Daļu saucēju vienādošana
"Ja divu daļu saucēji ir savstarpēji pirmskaitļi, tad to kopsaucējs (mazākais kopīgais dalāmais) ir abu saucēju reizinājums."
Dažreiz saka, ka saucējus raksta krustiski.
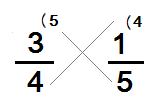
Piemērs:
Noteikt kopsaucēju daļām un
Noskaidro, vai saucēji 4 un 3 ir savstarpēji pirmskaitļi.
Skaitļa 3 dalītāji: 1; 3.
Skaitļa 4 dalītāji: 1; 2; 4.
Skaitļu 3 un 4 kopīgais dalītājs ir tikai skaitlis 1, tātad tie ir savstarpēji pirmskaitļi.
Skaitļa 3 dalītāji: 1; 3.
Skaitļa 4 dalītāji: 1; 2; 4.
Skaitļu 3 un 4 kopīgais dalītājs ir tikai skaitlis 1, tātad tie ir savstarpēji pirmskaitļi.
Daļa jāpaplašina ar 3, bet jāpaplašina ar 4
un , iegūto daļu saucēji ir vienādi (12)
Ievēro: ja abi saucēji ir pirmskaitļi, tad nav jāpārbauda kopīgie dalāmie. Šajā gadījumā abi saucēji vienmēr būs arī savstarpēji pirmskaitļi.
Atceries, pirmskaitļi ir: 2; 3; 5; 7; 11; 13; 17; 19; 23; 29;...
Piemērs:
Vienādo saucējus daļām un .
17 un 5 katrs ir pirmskaitlis (dalās tikai ar sevi un 1), tātad tie ir arī savstarpēji pirmskaitļi.
Tātad katru daļu paplašina ar otras daļas saucēju:
jāpaplašina ar 5, bet jāpaplašina ar 17
un , iegūto daļu saucēji ir vienādi (85).

