Datu grafiskie attēli histogramma un poligons parāda datu sadalījumu visā datu kopā.
Sadalījums var būt dažāds. Salīdzini 1. un 2. attēlu!
Sadalījums var būt dažāds. Salīdzini 1. un 2. attēlu!
1. attēls. Histogramma I
2. attēls. Histogramma II
2. attēlā redzams, ka, atšķirībā no 1. attēla, dati izkārtojušies simetriski ap kopas vidējo vērtību, proti, dati vairāk koncentrējas sadalījuma vidū, turklāt histogrammas malējie stabiņi ir īsāki nekā tie, kas atrodas vidū.
Datus, kas histogrammā sakārtojas simetriski ap kopas vidējo vērtību, sauc par normāli sadalītiem datiem.
Normālsadalījums ir matemātisks jēdziens, kas raksturo nejaušībai pakļautu notikumu iestāšanās relatīvo biežumu.
Ja līknei, kuru iegūst, apvelkot histogrammu, ir zvanveida forma, to sauc par normālā sadalījuma jeb Gausa līkni. Citiem vārdiem - normālā sadalījuma poligons ir Gausa līkne.
Gausa līknes forma ir atkarīga no diviem parametriem: vidējās vērtības un standartnovirzes .
1. Vidējās vērtības izmaiņas Gausa līkni pārvieto virzienā: ja pieaug, līkne pārvietojas pa labi, ja samazinās, - pa kreisi.
2. Standartnovirzes izmaiņas ietekmē līknes formu: standartnovirzes vērtībai pieaugot, līkne kļūst lēzenāka, bet, tai samazinoties, - stāvāka.
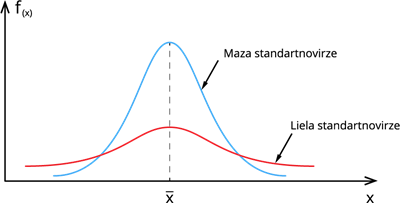
Ja mēs aplūkotu piemēru, kurā pa dienām pētīti naudas ieņēmumi kādā veikalā, tad mazas standartnovirzes gadījumā varētu teikt, ka ieņēmumi katru dienu ir ļoti līdzīgi. Ja standartnovirze ir liela, tad ienākumi nav stabili, pa dienām tie ir ļoti atšķirīgi.
Normālā sadalījuma gadījumā ir zināmas likumsakarības, cik daudz procentu no visām variantēm atrodas intervālos , , .
Normāli sadalītiem datiem ir spēkā normālsadalījuma \(1; 2\) un \(3\) standartnoviržu likums (empīriskais likums):
- \(68,28\)% visu datu atrodas vienas standartnovirzes attālumā no vidējās vērtības: .
-
\(95,45\)% visu datu atrodas divu standartnoviržu attālumā no vidējās vērtības: .
-
\(99,73\)% (gandrīz visi) datu kopas elementi atrodas trīs standartnoviržu attālumā no vidējās vērtības: .
Parasti šos procentus noapaļo līdz desmitdaļām.
Pareizi izvēloties izlasi (reprezentatīvu izlasi), aprēķinot standartnovirzi () un noskaidrojot izlases datu sadalījumu, var izdarīt secinājumus par pašu populāciju (ģenerālkopu).
Bet jāatceras, ka ar statistiskas metodēm iegūtiem pētījumu rezultātiem nekad nebūs \(100\)% ticamība.
Piemērs:
12.b klases skolēni eksāmenā vidēji ieguva \(80\) punktus un to standartnovirze bija \(3\) punkti. Izmantojot empīrisko likumu, novērtē eksāmena rezultātus, ja zināms, ka tiem ir normālais sadalījums.
Dots: .
1) Pēc empīriskā likuma, \(68,3\)% visu datu atrodas vienas standartnovirzes attālumā no vidējā aritmētiskā
punkti,
punkti.
Tātad \(68,3\)% skolēnu eksāmenā iegūto punktu skaits atrodas intervālā (\(77;83\)).
2) \(95,5\)% visu datu atrodas divu standartnoviržu attālumā no vidējās vērtības.
punkti,
punkti.
Tātad \(95,5\)% skolēnu eksāmenā iegūto punktu skaits atrodas intervālā (\(74;86\)).
3) \(99,7\)% visu datu atrodas divu standartnoviržu attālumā no vidējās vērtības.
punkti,
punkts.
Tātad \(99,7\)% skolēnu eksāmenā iegūto punktu skaits atrodas intervālā (\(71;89\)).
Papildini zināšanas!
Mācību video, kurā vari uzzināt vairāk par normālsadalījumu un standartnovirzes pielietojumu (11 min).
Vingrinies šīs tēmas 9.-12. uzdevumu! Izpēti atbilžu soļus!
