Funkcijas pētīšanas shēma — teorija. Matemātika (Skola2030), Matemātika II.

Video mācību materiāli

"MATEMĀTIKA II"

Vispārīgā funkcijas pētīšanas shēma

1. Atrod funkcijas definīcijas apgabalu.

2. Noskaidro, vai funkcija ir pāra vai nepāra.

3. Noskaidro, vai funkcija ir periodiska, atrod periodu.

4. Atrod funkcijas grafika krustpunktus ar koordinātu asīm un nosaka vienādzīmju intervālus, kuros funkcija ir pozitīva un kuros - negatīva (ja vienādojuma atrisināšana nerada grūtības).

5. Atrod 1. kārtas atvasinājumu, nosaka funkcijas augšanas un dilšanas intervālus un aprēķina ekstrēma punktu koordinātas.

6. Atrod 2. kārtas atvasinājumu, nosaka grafika izliekuma un ieliekuma intervālus un aprēķina pārliekuma punktu koordinātas.*

7. Atrod grafika asimptotas.**

8. Atrod funkcijas vienpusējās robežas definīcijas apgabala intervālu galos, atrod funkcijas vērtības pēc vajadzības izraudzītos papildpunktos.

Piemērs:

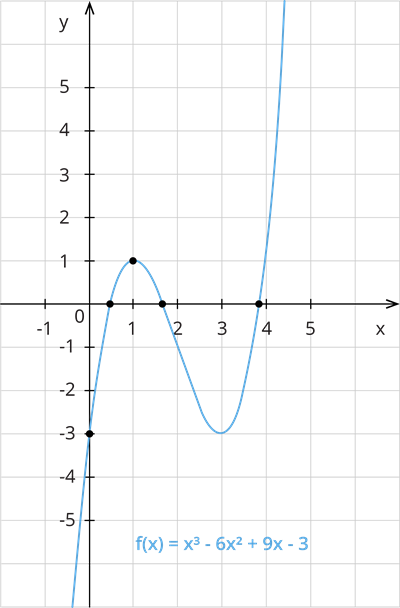
Konstruē funkcijas

y = x^{3} - 6 x^{2} + 9 x - 3

grafiku!

1. Funkcija ir definēta visām reālām $x$ vērtībām.

2. Funkcija nav ne pāra, ne nepāra

\begin{array}{l} f (- x) = {(- x)}^{3} - 6 {(- x)}^{2} + 9 (- x) - 3 = - x^{3} - 6 x^{2} - 9 x - 3 \\ f (- x) \neq f (x) \\ f (- x) = - (x^{3} + 6 x^{2} + 9 x + 3) \\ f (- x) \neq - f (x) \end{array}

3. Funkcija nav periodiska.

4. Krustpunkts ar $Oy$ asi, ja $x=0.$

f (0) = 0^{3} - 6 0^{2} + 9 \cdot 0 - 3 = - 3

Koordinātu asīs atliekam punktu $(0;-3).$

Lai noteiktu grafika krustpunktus ar $Ox$ asi, būtu jāatrisina vienādojums

x^{3} - 6 x^{2} + 9 x - 3 = 0

. Šajā gadījumā tas ir grūti, tāpēc to nedara.

5. Atvasina funkciju un atrod kritiskos punktus:

\begin{array}{l} y^{'} = {(x^{3} - 6 x^{2} + 9 x - 3)}^{'} = 3 x^{2} - 12 x + 9 \\ 3 x^{2} - 12 x + 9 = 0 \\ x^{2} - 4 x + 3 = 0 \\ x = 1, x = 3 \end{array}

$x$	$(- \infty; 1)$	$1$	$(1;3)$	$3$	$(3; + \infty)$
$f^{'} (x)$	$+$	$0$	$-$	$0$	$+$
$f(x)$	aug $↗$	max $(1;1)$	dilst $↘$	min $(3;-3)$	aug $↗$

Nosaka atvasinājuma zīmes intervālos, piemēram no

(- \infty; 1)

izvēlamies $x=0$.

f^{'} (0) = 3 \cdot 0^{2} - 12 \cdot 0 + 9 = 9 = (+)

Zīmju noteikšanu intervālos drīkst veikt galvā.

Pēc atvasinājuma zīmju maiņas, var secināt, ka $x=1$ ir maksimuma punkts un $x=3$ ir minimuma punkts.

Aprēķina funkcijas ekstrēmus - maksimumu un minimumu:

\begin{array}{l} f (1) = 1^{3} - 6 \cdot 1^{2} + 9 \cdot 1 - 3 = 1 \\ f (3) = 3^{3} - 6 \cdot 3^{2} + 9 \cdot 3 - 3 = - 3 \end{array}

Koordinātu plaknē atliekam punktus $(1;1)$ un $(3;-3). $

6. Nosaka 2. kārtas atvasinājumu, atrod pārliekuma punktus:

\begin{array}{l} f^{″} (x) = {(3 x^{2} - 12 x + 9)}^{'} = 6 x - 12 \\ 6 x - 12 = 0 \\ x = 2 \end{array}

$x$	$(- \infty; 2)$	$2$	$(2; + \infty)$
$f^{″} (x)$	$-$	$0$	$+$
$f(x)$	izliekta	$(2;-1)$	ieliekta

\begin{array}{l} f^{″} (- 10) = 6 \cdot (- 10) - 12 = (-) \\ f^{″} (10) = 6 \cdot 10 - 12 = (+) \end{array}

Pēc 2. kārtas atvasinājuma zīmēm, secinām, ka funkcijai ir pārliekuma punkts.

f (2) = 2^{3} - 6 \cdot 2^{2} + 9 \cdot 2 - 3 = - 1

Koordinātu plaknē atliek pārliekuma punktu $(2;-1).$

Izmantojot iegūtos datus, konstruē funkcijas grafiku.

Atrod funkcijas vērtības grafika precizēšanai:

\begin{array}{l} f (4) = 4^{3} - 6 \cdot 4^{2} + 9 \cdot 4 - 3 = 1 \\ f (5) = 5^{3} - 6 \cdot 5^{2} + 9 \cdot 5 - 3 = 17 \end{array}

*Informācija skolotājam

Pēc SKOLA2030 paraugprogrammas (51. -55. lpp.) vidusskolā 2. kārtas atvasinājumu nosaka tikai polinomiem.

**Vidusskolēnam nav jāprot noteikt slīpās asimtotas.

Rekomendācija - konstruēt tādas daļveida funkcijas, kurām nav pārliekuma punktu un nav slīpo asimptotu.

Piemēram, $y = \frac{ax}{b - c x^{2}}; y = \frac{ax}{{cx}^{2} - b}; y = \frac{a x^{2} + b}{c x^{2} + d}; y = \frac{a x^{2} - b}{c x^{2} - d}$ .

Atsauce:

Materiālu sagatavoja Mg. math. Laima Baltiņa

Dainis Kriķis. Kārlis Šteiners. Matemātiskās analīzes elementi vidusskolai. 1. daļa. izm. 171. lpp.

Iepriekšējā teorija

Atgriezties tēmā

Nākamā teorija

Nosūtīt atsauksmi

Atradi kļūdu?

Sūti mums ziņu!

Video mācību materiāli

"MATEMĀTIKA II"

PALĪGSMĀCĪBĀS.LV

\(x\)	$(- \infty; 1)$	\(1\)	\((1;3)\)	\(3\)	$(3; + \infty)$
$f^{'} (x)$	\(+\)	\(0\)	\(-\)	\(0\)	\(+\)
\(f(x)\)	aug $↗$	max \((1;1)\)	dilst $↘$	min \((3;-3)\)	aug $↗$

\(x\)	$(- \infty; 2)$	\(2\)	$(2; + \infty)$
$f^{″} (x)$	\(-\)	\(0\)	\(+\)
\(f(x)\)	izliekta	\((2;-1)\)	ieliekta

3. Funkcijas pētīšanas shēma

Teorija