Vienādojuma sin x=a atrisināšana no vienības riņķa

ONLINE VIDEO KURSS

"MATEMĀTIKA 11. KLASEI"

Vienādojumu $sinx=a$ ērti atrisināt, izmantojot vienības riņķa līniju. Trigonometriskais vienības riņķis ir dots matemātikas eksāmena formulu lapā.

Atrisināsim vienādojumu

\sin x = \frac{\sqrt{3}}{2}

Uzzīmē vienības riņķa līniju, uz sinusu ass atliek vērtību

\frac{\sqrt{3}}{2}

Iezīmē tos pagrieziena leņķus, kuru sinuss ir

\frac{\sqrt{3}}{2}

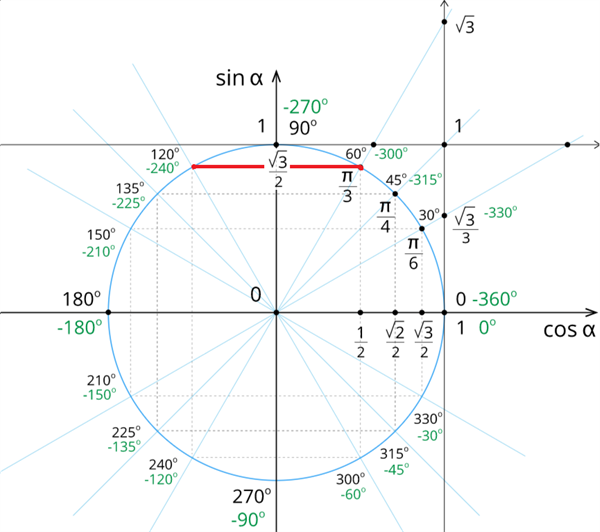
Ievēro, ka pagrieziena leņķim pieskaitot vai atņemot vienu vai vairākas reizes pilnu leņķi (periods

360 °

jeb

2 π

), atkal nonāksim tajā pašā vienības riņķa punktā. Tāpēc vienādojumam

\sin x = \frac{\sqrt{3}}{2}

ir bezgalīgi daudz atrisinājumu un tie ir:

\begin{array}{l} x = [\begin{array}{l} 60^{o} + 360^{o} n \\ 120^{o} + 360^{o} n \end{array} \\ kur n \in ℤ \end{array}

Atbildi var pierakstīt radiānos:

x = [\begin{array}{l} \frac{π}{3} + 2 π n \\ \frac{2 π}{3} + 2 π n \end{array}

Piemērs:

Atrisini vienādojumu

\begin{array}{l} \sin x = - \frac{\sqrt{3}}{2} \\ x = [\begin{array}{l} {- 60}^{o} + 360^{o} n \\ 240^{o} + 360^{o} n \end{array} \\ x = [\begin{array}{l} - \frac{π}{3} + 2 π n \\ \frac{4 π}{3} + 2 π n, n \in ℤ \end{array} \end{array}

n \in ℤ

nozīmē, ka $n$ vērtības ir visi veselie skaitļi.

Iegaumē sekojošu pamatvienādojumu atrisinājumus:

$\sin x=1$. Atrisinājums ir $x = \frac{π}{2} + 2 π n$ jeb $x = 90^{o} + 360^{o} n$ , $n \in ℤ$
$\sin x=0$. Atrisinājums ir $x = π n$ jeb $x = 180^{o} n$

$\sin x = -1$. Atrisinājums ir $x = - \frac{π}{2} + 2 π n$ jeb $x = - 90^{o} + 360^{o} n$

Atceries! Vienādojumam $\sin x = a$ eksistē atrisinājums tikai tad, ja $-1\leq a \leq 1$ jeb $|a|\leq 1$.

Vienības riņķis formulu lapā

Atradi kļūdu?

ONLINE VIDEO KURSS

"MATEMĀTIKA 11. KLASEI"

1. Vienādojuma sin x=a atrisināšana no vienības riņķa