Liels skaits nesakārtotu datu nedod uzskatāmu priekšstatu par to sadalījumu. Lai datus varētu analizēt, tos sakārto.
Kvantitatīvus un kategoriālus datus parasti attēlo biežuma tabulā.
Piemērs:
Piemēram, vērojot pretim braucošo automašīnu krāsu, iegūstam datus - t.i. katrai automašīnai atbilstošo krāsu.
Šo kategoriālo datu atbilstošā biežumu tabula izskatīsies šādi:
| Krāsa | Balta | Melna | Sarkana | Zila |
|
Absolūtais
biežums
|
9
|
5
|
4
|
2
|
Skaitļi šajā tabulā nav dati, bet gan novērojumu skaits jeb biežums. Biežums ļauj spriest par datu sadalījumu.
Par histogrammu sauc diagrammu, kuru veido taisnstūri, kuru pamati ir vienādi ar biežuma klašu garumu, bet augstumi - ar attiecīgā intervāla absolūto vai relatīvo biežumu.
Zīmējot histogrammu, taisnstūru pamati parasti tiek atlikti uz horizontālās (abscisu) ass, bet augstumi - uz vertikālās (ordinātu) ass.
Piemērs:
Tika veikta vidusskolēnu aptauja (aptaujāti 80 skolēni) par naudas summām, ko viens skolēns vidēji tērē ikdienas pusdienu iegādei.
Iegūtie dati ir attēloti histogrammā:
Histogrammas parasti izvēlas nepārtrauktu un grupētu datu attēlošanai.
Histogrammas pirmā un pēdējā stabiņa platumu izvēlas vienādu ar pārējo stabiņu platumu, ja arī intervāla garums ir atšķirīgs.
Poligons ir lauzta līnija, kuras virsotnes koordinātu plaknē ir punkti, kuru abscisa ( koordināta) atbilst pazīmes vērtībai, bet ordināta ( koordināta) - šīs pazīmes vērtības biežumam.
Poligonu zīmējot, pieņemts abos poligona galos pievienot punktu, kurā biežums ir .
Piemērs:
11. klases skolēni kārtoja eksāmenu angļu valodā. Rezultāti ir attēloti biežuma tabulā, un, vadoties pēc tabulas datiem, ir konstruēts poligons.
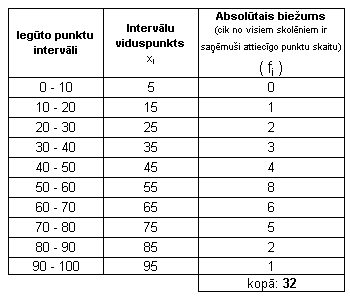
Poligons:
Poligonu var konstruēt, izmantojot gan absolūto, gan relatīvo biežumu.
Piemērs:
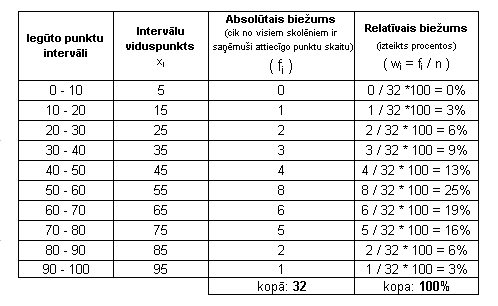
Poligons, kurā izmantots relatīvais biežums:
Ja ir uzzīmēta datu histogramma, poligonu var iegūt, savienojot stabiņu augšējo malu viduspunktus un pirmā un pēdējā stabiņa apakšējās malas ārējās virsotnes.
