4. Absolūtā kļūda neregulāri mainīga fizikālā lieluma gadījumā

Ja, mērot strāvas stiprumu rezistora ķēdē ar sensoru 1 sekundē, iegūti šādi rezultāti:

 

 

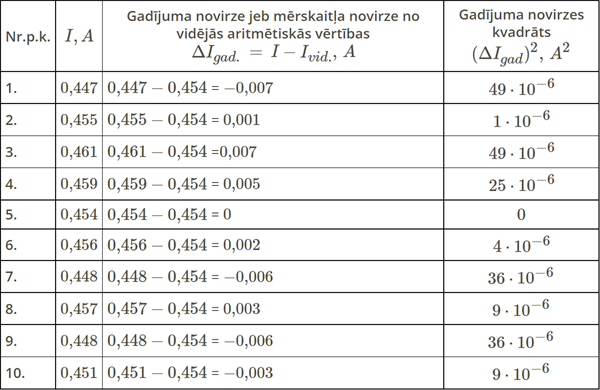
Aprēķinam vidējo aritmētisko vērtību:

 

$\frac{(\mathrm{0,447}+\mathrm{0,455}+\mathrm{0,461}+\mathrm{0,459}+\mathrm{0,454}+\mathrm{0,456}+\mathrm{0,448}+\mathrm{0,457}+\mathrm{0,448}+\mathrm{0,451})}{\mathrm{10}}$ = 0,454 \(A\)

 

Aprēķinām gadījuma noviržu kvadrātu summu:

 

$\sum ({({\mathrm{\Delta }I}_{\mathit{gad}})}^2)$ = $\mathrm{(49+1+49+25+0+4+36+9+36+9)}·{10}^{-6}$= $218·{10}^{-6}$ $A^2$

 

Strāvas stipruma absolūto aprēķinam pēc formulas $\mathrm{\Delta }I=k\cdot \sqrt{\frac{{({\mathrm{\Delta }I}_{\mathit{gad}})}^2}{n\cdot (n-1)}}$, kur \(k\) — Stjūdenta koeficients un \(n\) — mērījumu skaits.

 

Stjūdenta koeficients ir atkarīgs no mērījumu skaita un ticamības varbūtības (sk.tabulas fragmentā).

 

Mērījumu skaits	Ticamības varbūtība 90%	Ticamības varbūtība 95%	Ticamības varbūtība 99%
10	1,833	2,262	3,250
11	1,812	2,228	3,169
12	1,796	2,201	3,106
13	1,782	2,179	3,055
14	1,771	2,160	3,012
15	1,761	2,145	2,977

 

Aprēķinam strāvas stipruma absolūto kļūdu, ja ticamības varbūtība ir 90%

 

$\mathrm{\Delta }I=k\cdot \sqrt{\frac{{({\mathrm{\Delta }I}_{\mathit{gad}})}^2}{n\cdot (n-1)}}$ = $\mathrm{1,833}·\sqrt{\frac{218·{10}^{-6}}{10·(10-1)}}$ = 0,002 \(A\)

 

Tātad, mērījuma rezultāts \(I\)\(= (\)$\mathrm{0,454}\pm \mathrm{0,002}$\()\)\(A\) un strāvas stipruma patiesās vērtības intervāls ir \([\)\(0,452; 0,456]\)\(A\). Tas nozīmē, ka, mērot strāvas stiprumu 100 reizes, 90 gadījumos iegūst strāvas stipruma vērtību, kas atrodas \([\)\(0,452: 0,456]\) intervālā.

 

Ticamības varbūtībai 95% atbilst absolūtā kļūda:

 

$\mathrm{2,262}·\sqrt{\frac{218·{10}^{-6}}{10·(10-1)}}$ = 0,004 \(A\) un patiesās vērtības intervāls \([\)\(0,450; 0,458]\).

 

Mērot strāvas stiprumu 100 reizes, strāvas stipruma vērtība 95 reizes atradīsies šajā intervālā.

 

Ticamības varbūtībai 99% atbilst absolūtā kļūda:

 

$\mathrm{3,25}·\sqrt{\frac{218·{10}^{-6}}{10·(10-1)}}$ = 0,005 \(A\).

 

No 100 mērījumiem 99 reizes strāvas stipruma vērtība būs intervālā \([\)\(0,449; 0,459]\).