Par taisnstūri sauc paralelogramu, kuram visi leņķi ir taisni.

Tā kā taisnstūris ir paralelograms, tam piemīt visas paralelograma īpašības.
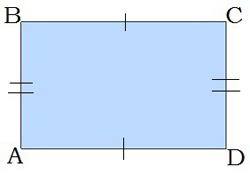
Taisnstūra pretējās malas ir pa pāriem vienāda garuma: \(AB = CD\) \(BC = AD\) |
 |
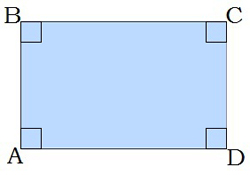
Taisnstūrim visi leņķi ir vienādi ar \(90\). Tātad, acīmredzami, ka taisnstūra pretējie leņķi ir vienāda lieluma un taisnstūra katras malas pieleņķu summa ir \(180\) grādi. |
 |
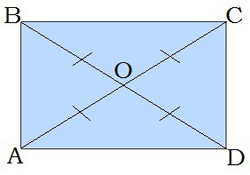
Taisnstūra diagonāles krustpunktā dalās uz pusēm: \(BO = OD\) \(AO = OC\) Un arī \(BO = OD = AO = OC\). |
 |
Taisnstūra diagonāle sadala to divos vienādos trijstūros, pie tam taisnleņķa trijstūros. |
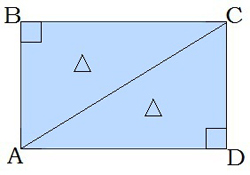 |
| Šķērsleņķi pie diagonāles ir vienādi. | 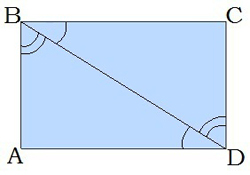 |
Taisnstūrim piemīt arī īpašība, kura ir spēkā tikai taisnstūrim.
Taisnstūra diagonāles ir vienāda garuma: \(BD = AC \) | 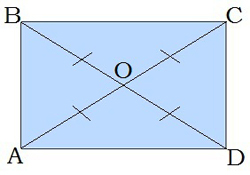 |