Trigonometriskās sakarības taisnleņķa trijstūrī lieto, lai aprēķinātu tā malas vai šauros leņķus.
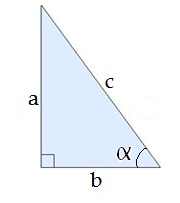
Padomi, kā izvēlēties pareizo funkciju:
- Noskaidro, vai ir nepieciešams izmantot hipotenūzu (dota vai jāaprēķina).
Ja izmanto hipotenūzu, tad lieto sinusu vai kosinusu. Ja izmanto tikai katetes, tad lieto tangensu. - Ja izmanto kateti, noskaidro, vai izmanto to kateti, kas ir pretī leņķim (zīmējumā tā ir ).
Ja izmanto pretkateti, tad lieto sinusu. Ja neizmanto pretkateti, tad lieto kosinusu.
Ja trijstūrī ir doti abi šaurie leņķi, labāk zīmējumā ieraksti tikai vienu leņķi, lai viennozīmīgi saprastu, kura ir piekatete, kura pretkatete.
Svarīgi!
Hipotenūza vienmēr ir saucējā (daļas apakšā).
Trigonometrisko funkciju vērtības (kuras ir jāzina no galvas)
1 |
Pārējiem leņķiem vērtības var atrast tabulās un aprēķināt ar kalkulatoru. Aptuveni novērtēt trigonometrisko funkciju vērtības var, izmantojot trigonometrisko vienības riņķi.
Piemērs:
Aprēķini taisnleņķa trijstūra šauro leņķi!
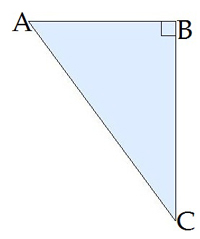
Dots: cm, cm
Jāaprēķina:
Risinājums:
Redzam, ka jāizmanto hipotenūza, tātad tas būs sinuss () vai kosinuss ().
Leņķim dotā katete ir pretim, tātad tas būs sinuss, hipotenūzai jābūt saucējā.
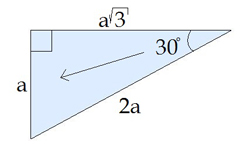
Izmantojot un funkcijas, var iegūt sakarības:
- Katete, kas atrodas pretī leņķim, ir puse no hipotenūzas.
- Kateti, kas atrodas pretī leņķim iegūst, īsāko kateti pareizinot ar .
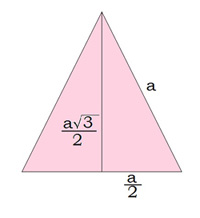
Iepriekšminēto sakarību ērti izmantot, aprēķinot regulāra trijstūra augstumu.
Kā zināms, regulāra trijstūra visi leņķi ir un bisektrise leņķi sadala uz pusēm.
Kā zināms, regulāra trijstūra visi leņķi ir un bisektrise leņķi sadala uz pusēm.
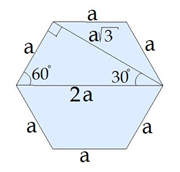
Ievēro, ka regulārā sešstūrī garākā sešstūra diagonāle, īsākā diagonāle un mala veido taisnleņķa trijstūri, kurā ir leņķis.
Interesanti:
- Trigonometrija no grieķu valodas nozīmē trijstūris + mērīt, to pazina un izmantoja astronomijā jau pirms mūsu ēras.
- Vārds "sinuss" cēlies no latīņu vārda izliekums, dobums.
- Vārds "kosinuss" - sinusa papildinājums.
- Vārds "tangenss" nozīmē - tāds, kas pieskaras.