Par funkcijas \(y=f(x)\) nullēm sauc tās argumenta \(x\) vērtības, ar kurām funkcijas vērtība vienāda ar nulli: \(f(x)=0\).
Funkcijas grafiks krusto abscisu asi (\(x\) asi) punktos, kas ir funkcijas nulles.
Lai noteiktu funkcijas nulles pēc grafika, nosaka visus krustpunktus ar \(x\) asi.
Kad ir noteiktas funkcijas nulles, var noteikt intervālus, kuros funkcijas vērtības ir ar vienādām zīmēm. Intervālā starp divām blakus esošām funkcijas nullēm funkcija ir vai nu pozitīva \(f(x)>0\), vai arī negatīva \(f(x)<0\).
Funkcija ir pozitīva (\(f(x)>0\)) visām tām \(x\) vērtībām, ar kurām grafiks atrodas virs \(x\) ass.
Vienādzīmju intervālu, kurā \(f(x)>0\), nosaka šādi:
- grafikā skatās to grafika daļu, kas atrodas virs \(x\) ass,
- nolasa visas atbilstošās \(x\) vērtības,
- uzraksta atbilstošo intervālu.
Piemērs:
Pēc dotā funkcijas \(f(x)\) grafika nosaki
1. funkcijas nulles
2. tās argumenta vērtības, ar kurām \(f(x)>0.\)
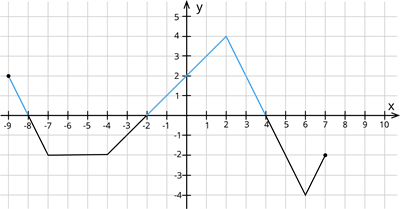
1. Pēc dotā grafika \(f(x)=0\), ja \(x=-8, x=-2, x=4\).
2. Dotajā zīmējumā \(f(x)>0\) vērtības ir iekrāsotas zilā krāsā.
\(f(x)>0\), ja
Ievēro, ka grafika galos ir punkti, funkcija ir ierobežota, tāpēc intervāla sākumpunkts pie skaitļa \(-9\) ir ar kvadrātiekavu.
Funkcija ir negatīva (\(f(x)<0\)) visām tām \(x\) vērtībām, ar kurām funkcija atrodas zem \(x\) ass.
Vienādzīmju intervālu, kurā \(f(x)<0\), nosaka šādi:
- grafikā skatās to grafika daļu, kas atrodas zem \(x\) ass,
- nolasa visas atbilstošās \(x\) vērtības,
- uzraksta atbilstošo intervālu.
Piemērs:
Pēc dotā funkcijas \(f(x)\) grafika nosaki tās argumenta vērtības, ar kurām \(f(x)<0\)!

Zīmējumā \(f(x)<0\) vērtības ir iekrāsotas zilā krāsā.
\(f(x)<0\), ja .
Ievēro, ka grafika galos ir punkti, funkcija ir ierobežota, tāpēc intervāla galapunkts pie skaitļa \(10\) ir ar kvadrātiekavu.