Funkcionālo sakarību starp mainīgajiem \(x\) un \(y\), kas izsakāma formā , sauc par apgriezto proporcionalitāti.
Funkcijas grafiks ir līkne, ko sauc par hiperbolu.
Tās īpašības:
- Definīcijas apgabals ir visi reālie skaitļi, izņemot 0:
- Vērtību apgabals arī ir visi reālie skaitļi, izņemot 0:
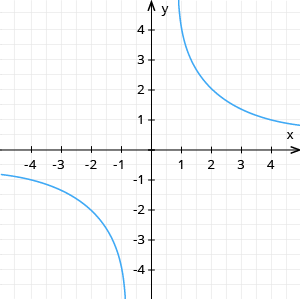
Ja \(a > 0\), tad hiperbolas zari atrodas I un III kvadrantā, funkcija ir dilstoša (1. piem.).
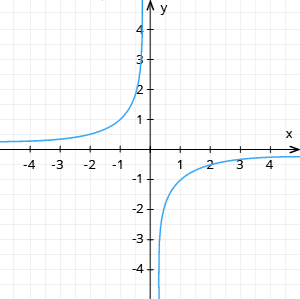
Ja \(a < 0\), tad hiperbolas zari atrodas II un IV kvadrantā, funkcija ir augoša (2. piem.).
Tā ir nepāra funkcija, tādēļ ir simetriska pret koordinātu sākumpunktu \((0; 0)\).
Lai konstruētu grafiku, sastāda vērtību tabulu, kurā izvēlas gan pozitīvus, gan negatīvus skaitļus.
Piemērs:
1. Konstruē grafiku funkcijai !
|  |
2. Konstruē grafiku funkcijai !
|  |