Par vektoru un summu sauc vektoru, kas vērsts no vektora sākuma punkta uz vektora beigu punktu, ja ir nofiksēts vektora sākuma punkts un vektors ir atlikts no vektora beigu punkta.
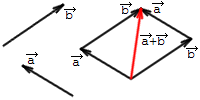
Šo saskaitīšanas veidu bieži sauc par trijstūra metodi.
Kā redzams, summas vektors ir vienāds ar vektoru, ko iegūst, ja abus saskaitāmos vektorus atliek no viena punkta un tad novelk iegūtā paralelograma diagonāli no šī kopīgā sākuma punkta. Šo sakarību bieži sauc par paralelograma likumu.
Vairāk nekā divu vektoru gadījumā ir spēkā daudzstūra likums.
Par vairāku vektoru summu sauc vektoru, kas vērsts no pirmā vektora sākuma punkta uz pēdējā vektora beigu punktu, ja ir nofiksēts pirmā vektora sākuma punkts un katrs nākamais vektors ir atlikts no iepriekšējā vektora beigu punkta.
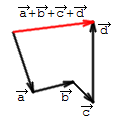
Svarīgi!
Vektoru summa nav atkarīga no saskaitāmo secības.
Svarīgi!
Pretēju vektoru summa ir nulles vektors: .
Svarīgi!
Pieskaitot vektoram nulles vektoru, summā sanāk sākotnējais vektors: .
Piemērs:
1) Jāaprēķina summa . Abi vektori jau atlikti vajadzīgajā veidā, tāpēc var izmantot trijstūra likumu. Summas vektors ir vērsts no pirmā vektora sākuma punkta uz otrā vektora beigu punktu . Tātad .
Piemērs:
2) Jāaprēķina summa . Te jāmaina saskaitāmo secība un jāpielieto trijstūra likums: .
Piemērs:
3) Jāaprēķina summa . Te var samainīt vietām saskaitāmos un tad izmantot daudzstūra likumu: .
Piemērs:
4) Dots paralēlskaldnis (zīmējumā). Jāaprēķina summa .
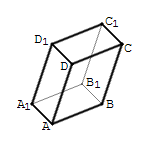
Otrais un trešais saskaitāmais ir pretēji vektori, tāpēc to summa ir nulles vektors: .
Tad (jo nulles vektora pieskaitīšana neko nemaina).
Tālāk - vektors ir vienāds ar vektoru , tāpēc var aizvietot un tad veikt saskatīšanu: .