Saīsinātās reizināšanas formulas ________________________________ Kvadrāttrinoms | Kvadrātvienādojums | Modulis |
Aritmētiskā progresija | Ģeometriskā progresija | Bezgalīgi dilstoša ģeometriskā progresija |
Sakņu īpašības | Pakāpju īpašības | Logaritmu īpašības |
Kombinatorika | Varbūtību teorija , - labvēlīgo notikumu skaits, - visu iespējamo notikumu skaits. , kur , - nesavienojami notikumi. , kur , - neatkarīgi notikumi. |
Trigonometrija
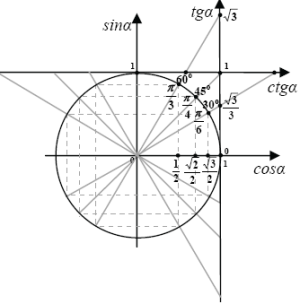 |