Skaitļu asi izmanto, lai uz tās attēlotu skaitļus, kam ir noteikts lielums.
Attālums starp skaitļiem ir vienāda lieluma. No kreisās puses uz skaitļu ass vienmēr atrodas mazāki skaitļi, bet no labās puses atrodas lielāki skaitļi. Bulta norāda, uz kuru pusi tiek atlikti lielāki skaitļi.

Zīmējot skaitļu asi, izvēlas skaitli, no kura sāk atlikt skaitļus uz ass, kā arī nosaka soļa jeb vienības attālumu starp skaitļiem. Skaitļu asī sākumpunkts var būt jebkāds skaitlis, ne vienmēr skaitļu ass sāksies ar \(0\).
Piemērs:
Šajā piemērā skaitlis tiek atlikts sākot ar \(0\), bet solis jeb vienība, kas tiek izmantota, lai atliktu skaitļus vienu aiz otra ir \(10\). Tātad, katrs nākamais skaitlis ir par \(10\) lielāks nekā iepriekšējais skaitlis.
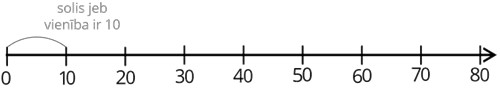
Šajā piemērā skaitlis tiek atlikts sākot ar \(15\), bet solis jeb vienība, kas tiek izmantota, lai atliktu skaitļus vienu aiz otra ir \(5\). Tātad, katrs nākamais skaitlis ir par \(5\) lielāks nekā iepriekšējais skaitlis.
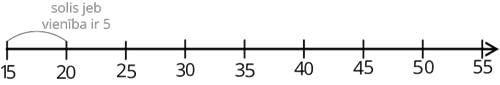
Izpratne par skaitļu asi ir vajadzīga, lai varētu nolasīt dažādu mērinstrumentu rādījumus ne tikai matemātikā, bet arī sadzīvē.

Skaitļu salīdzināšanai jāņem vērā,cik ciparu ir katrā skaitlī. Ja abiem skaitļiem ir vienāds ciparu skaits, tad jāsalīdzina dotie cipari katrā šķirā.
Piemērs:
Kurš skaitlis lielāks: \(9753\) vai \(9653\)?
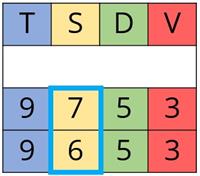
Sākot no kreisās puses, nosaka vai dotajā skaitļu sastāvā cipari ir vienādi vai atšķiras. Ja kādā no šķirām cipari atšķiras, tad secina, ka lielāks ir tas skaitlis, kuram atbilstošās šķiras cipars ir lielāks.
Šajā piemērām redzam, ka abiem skaitļiem tūkstošu šķira ir vienāda (\(9\)), bet simtu šķira atšķiras. Līdz ar to, lielāks ir tas skaitlis, kuram simtu šķira ir lielāka. Tātad \(9753 > 9653\)

