Fizikā ar jēdzienu "Darbs" saistās process, kurā kāds ķermenis tiek pārvietots tām pieliktā spēka iedarbības rezultātā. Ja ķermenim pieliktais spēks ir konstants un pārvietojuma virziens sakrīt ar pieliktā spēka virzienu, tad spēka veikto darbu var aprēķināt pēc formulas: \(A=F\cdot s\). Darba mērvienība SI vienībās ir džouls \(\mathrm{J}\).
Termodinamikā darbs tiek veikts tikai tad, kad mainās gāzes tilpums.
Pieņemts, ka:
- gāzes darbs ir pozitīvs, ja gāze, veicot darbu, izplešas: \(A>0\);
- gāzes darbs ir negatīvs, ja ārējo spēku iedarbībā gāze tiek saspiesta: \(A<0\). Šajā gadījumā gāze darbu neveic, jo darbu veic ārējais spēks, saspiežot gāzi.
Ja gāzes tilpums nemainās, tad gāze darbu neveic. \(A=0\).
Mainoties gāzes tilpumam, iespējams, mainās arī citi gāzes termodinamiskie parametri: spiediens \(p\) un temperatūra \(T\).
Apskatīsim gadījumu, kad gāze, to sildot cilindrā, pārvieto virzuli pie nemainīga spiediena (tādu procesu sauc par izobārisko procesu).
Gāzes darbs izobāriskā procesā, gāzei izplešoties - spiediens \(p\) nemainīgs.
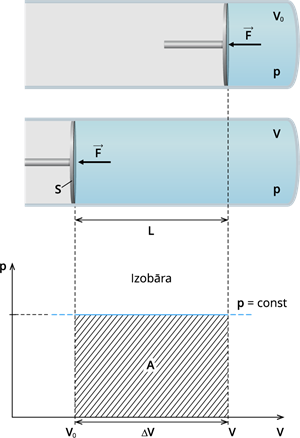
Darbs \(A\) šajā gadījumā tiek veikts, spēka \(F\) iedarbības rezultātā pārvietojot virzuli attālumā \(L\). Spēku \(F\) rada gāze, iedarbojoties uz virzuli ar spiedienu \(p\). Spēka lielumu varam aprēķināt šādi:
\(F=pS\), kur \(S\) virzuļa šķērsgriezuma laukums.
Ja šī spēkā iedarbībā virzulis tiek pārvietots attālumā \(L\), tad gāzes veiktais darbs \(A\) ir:
\(A=FL=pSL\).
Reizinājums \(SL\) ir gāzes tilpuma pieaugums \(ΔV\) un sakarība gāzes darba aprēķināšanai izobāriskā procesā ir \(A=p\Delta V\).
Ja apskatām izobāru zīmējumā, tad varam secināt, ka gāzes veiktais darbs ir skaitliski vienāds ar iesvītrotās figūras laukumu!
Vēl vienu sakarību gāzes darba aprēķināšanai, ja zināma gāzes temperatūras maiņa izobāriskā procesā, var iegūt izmantojot Mendeļējeva-Klapeirona vienādojumu, ar to aprakstot divus gāzes stāvokļus:
šeit:
- gāzes sākuma un beigu tilpumi, \(\mathrm{m^3}\)
- gāzes daudzums, \(\mathrm{mol}\)
- gāzes sākuma un beigu temperatūras, \(\mathrm{K}\)
\(R\) - gāzu molārā konstante, \(R=8,31\mathrm{\frac{J}{mol\cdot K}}\).
Izdarīsim algebriskus pārveidojumus, atņemot no otrā vienādojuma pirmo, un vienkāršosim, izmantojot zināmas sakarības: