Kā izpildīt reizināšanu ?
Uzzīmēsim taisnstūri un pa horizontāli šo vienu veselo taisnstūri sadalīsim \(5\) kolonnās, bet pa vertikāli \(4\) rindiņās. Taisnstūris sadalīts vienādās rūtiņās ar malām no taisnstūra garuma un no taisnstūra platuma un vienas rūtiņas laukums ir no lielā taisnstūra laukuma. Ņemtais taisnstūris ar malām un no lielā taisnstūra (zīmējumā oranžā krāsā) sastāv no rūtiņām, tāpēc tā laukums ir no lielā taisnstūra laukuma.
Tagad nepieciešams saprast, kā no un "izveidot" daļu .
Ir redzams, ka un .

Ieguvām divu daļu reizināšanas likumu:
1. Sareizina saucējus, lai iegūtu, cik daļās jeb rūtiņās ir sadalīts veselais.
2. Sareizina skaitītājus, lai iegūtu, cik liels ir iekrāsotais rūtiņu laukums.
3. Saīsina daļu, ja tas ir iespējams.
Svarīgi!
Divu parasto daļu reizinājums ir parastā daļa, kuras skaitītājs ir vienāds ar doto daļu skaitītāju reizinājumu un saucējs ir vienāds ar doto daļu saucēju reizinājumu.
, kur a, b, c, d ir naturālie skaitļi
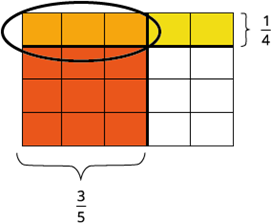
Varam spriest arī citādi. Sākumā aizkrāsosim (paņemsim) no lielā taisnstūra (pa horizontāli sadalīsim taisnstūri 5 vienādās daļās un paņemsim 3 tādas daļas). Un no iegūta taisnstūra ņemsim (sadalīsim pa vertikāli šo taisnstūri 4 vienādās daļās un paņemsim 1 tādu daļu). Šo darbību rezultātā iegūsim taisnstūri (zīmējumā ir apvilkts), kura laukums ir \(=\) .
Piemērs. Aprēķini reizinājumu !
1. Tieši kā pirmajā piemērā sadalīsim doto taisnstūri pa horizontāli \(7\) vienādās kolonnās, bet pa vertikāli \(3\) vienādās rindās. Tagad viens vesels taisnstūris sastāv no rūtiņām.
2. Pa horizontāli ņemsim \(4\) rūtiņas, bet pa vertikāli \(2\) rūtiņas. Pavisam ir ņemtas rūtiņas.
3. Iekrāsotais (tumši zils) rūtiņu laukums ir \(8\) rūtiņas no \(21\) rūtiņas vai . Daļu saīsināt nav iespējams. Tā arī ir atbilde.

Nav svarīgi, sākumā mēs taisnstūri sadalām vertikāli un pēc tam horizontāli vai sākumā horizontāli un pēc tam vertikāli, aizkrāsotā daļa (reizinājums) no tā nemainās.
Apskatīt, kā reizina veselo skaitļi ar daļu vai daļu ar daļu tu vari šeit: