Tāpat kā staru arī daudzstūri var pagriezt ap punktu. Tas attēlojas par tādu pašu daudzstūri, tikai citādāk novietots.
Trijstūra pagriešana ap virsotni par doto leņķi.
Attēlā ir redzams, kā trijstūri \(ABC\) pagriež ap virsotni \(C\) par \(50°\) un tas attēlojas par trijstūri \(\).

Izseko soļiem!
1. Sākotnējā trijstūra mala \(CA\) (sarkana) ap punktu \(C\) ir pagriezta par \(50°\). Tā attēlojas kā tumši zilā trijstūra mala \(\) (sarkana). Šo pārvietojumu vari redzēt uz transportiera, kas norādīts ar sarkano bultiņu.
2. Tāpat sākotnējā trijstūra mala \(CB\) (oranža) ap punktu \(C\) ir pagriezta par \(50°\). Tā attēlojas kā zilā trijstūra mala \(\) (oranža).
3. Un katra trijstūra trešā mala (zila) savieno abu pirmo malu galapunktus.
Taisnstūra pagriešana rūtiņu tīklā ap virsotni par \(90°\).
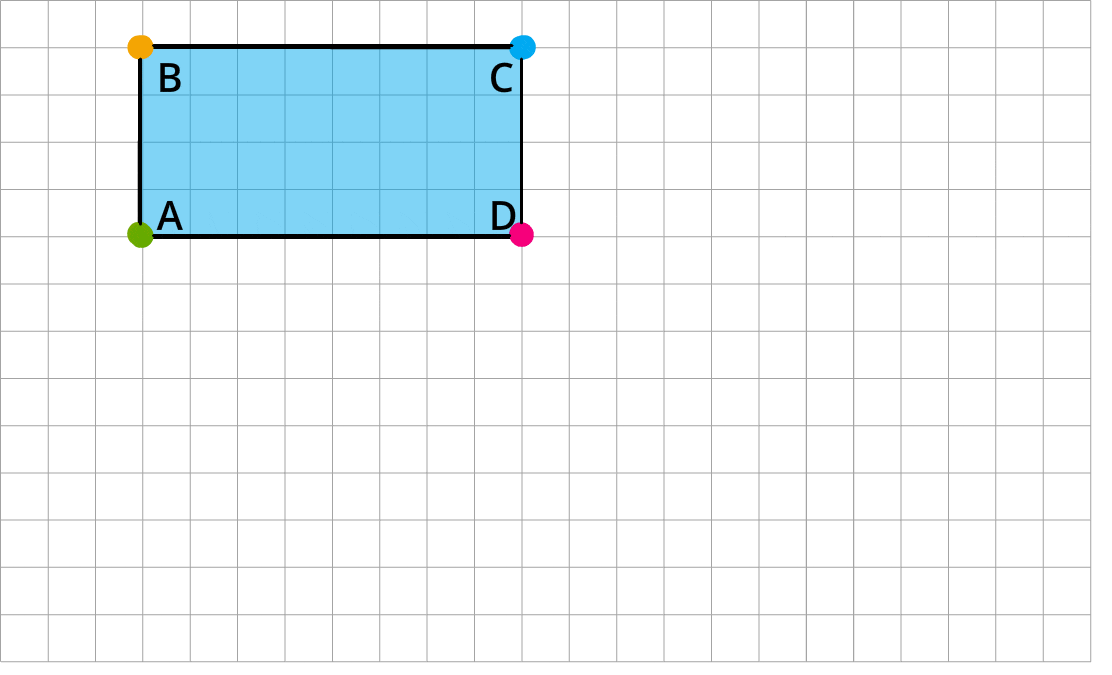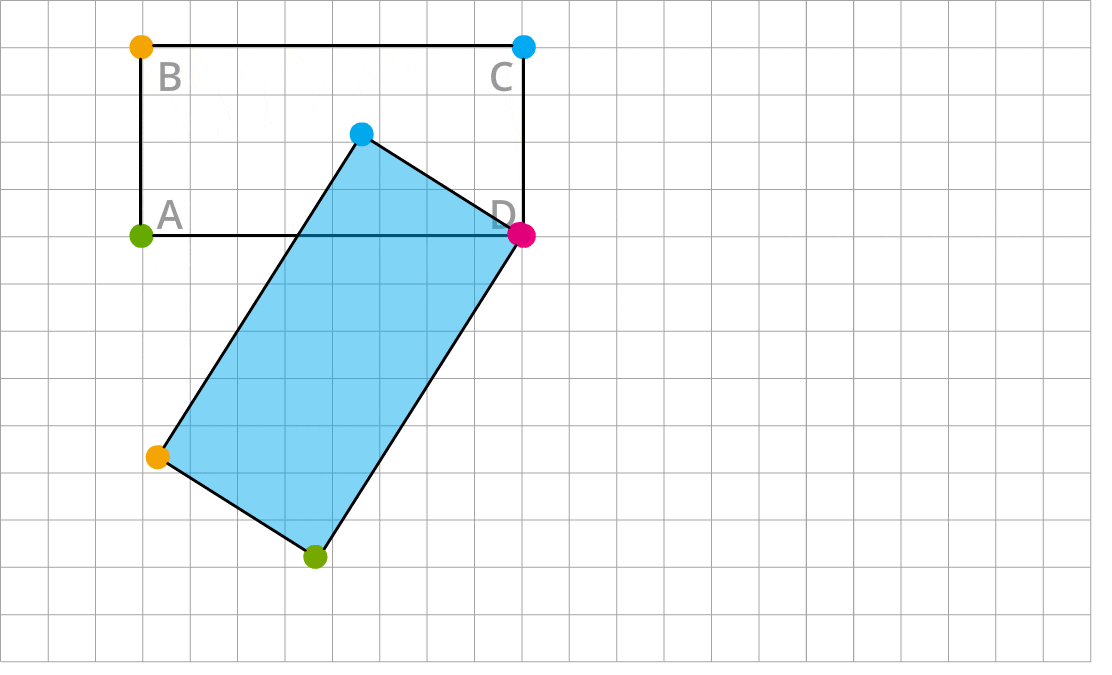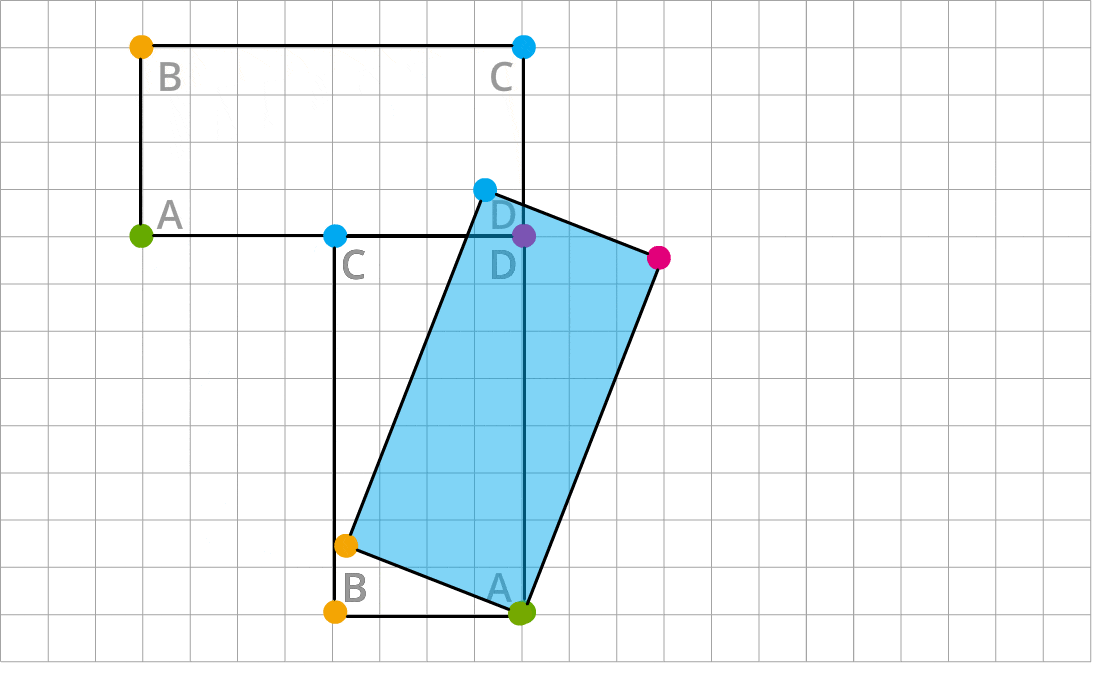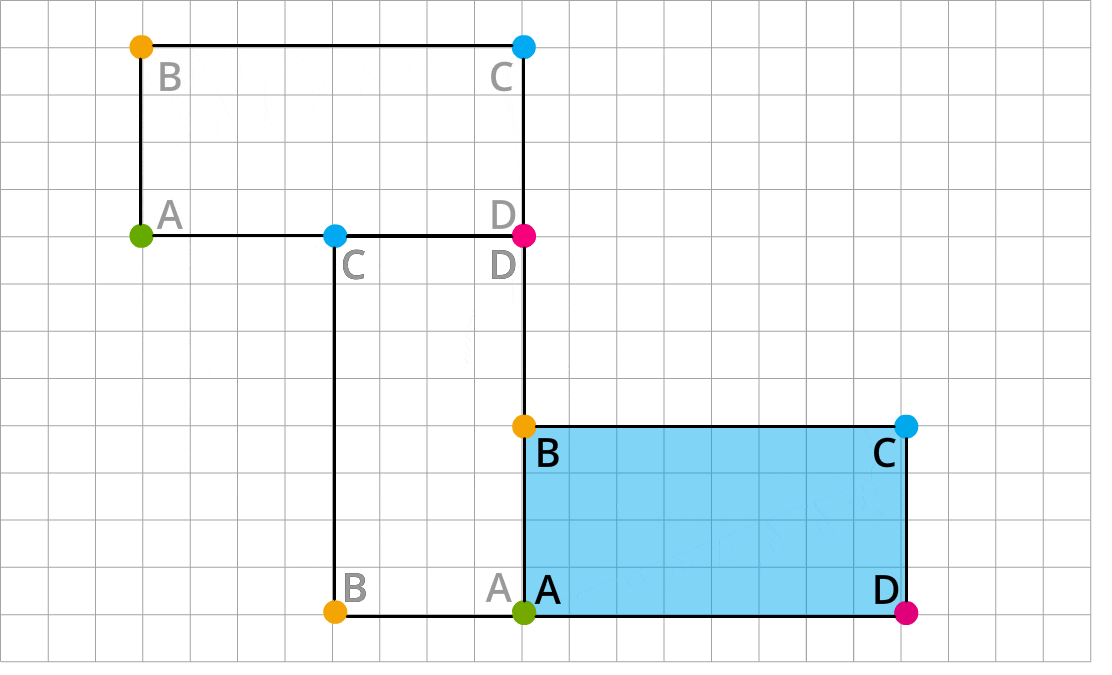
Izpēti, kā rūtiņu tīklā ir taisnstūris ABCD ir pagriezts divas reizes par \(90°\). Vispirms ap sarkano virsotni \(D\), pēc tam ap zaļo virsotni \(A\).

Svarīgi!
Taisnstūri pagriežot ap virsotni par \(90°\), tas katrā pagriezienā maina novietojumu no vertikāla uz horizontālu, no horizontāla uz vertikālu.
Zemāk dotais taisnstūris ir pagriezts par \(90°\) ap vienu un to pašu virsotni divas reizes.

Taisnstūru (vai citu daudzstūru pagriešanu) ap virsotni vari darīt praktiski!
1. Izgriez daudzstūri no izturīgāka papīra.
2. Pie transportiera centra vai uz rūtiņu lapas uzliec izgriezto daudzstūri.
1. Izgriez daudzstūri no izturīgāka papīra.
2. Pie transportiera centra vai uz rūtiņu lapas uzliec izgriezto daudzstūri.
3. Cirkuļa spico kāju iedur daudzstūra virsotnē un griez daudzstūri ap to! Vēro novietojumu!