Aksiāli simetriskas figūras
"Figūru, kas aksiālajā simetrijā pret kādu taisni attēlojas pati par sevi, sauc par aksiāli simetrisku figūru."
Figūrām var būt vairākas simetrijas asis.
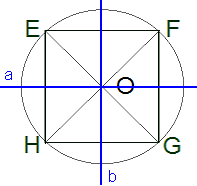
| EG - kvadrāta (arī riņķa) simetrijas ass FH - kvadrāta (arī riņķa) simetrijas ass a, b - kvadrāta (arī riņķa) simetrijas asis Kvadrātam kopā ir 4 simetrijas asis (a, b, kā arī taisnes, kas iet caur kvadrāta diagonālēm - EG un FH). Riņķim simetrijas ass ir diametrs, tāpēc riņķim ir bezgalīgi daudz simetrijas asis, jo var novilkt bezgalīgi daudz diametru. |
Aksiālās simetrijas piemēri ir daudzu jo daudzu celtņu fasādes, piemēram, Malnavas muiža Latvijā.

Pasaulē ievērojams ar savu simetriju ir Tadžmahala mauzolejs Indijā.

Atsauce:
http://lv.wikipedia.org/wiki/Att%C4%93ls:Malnava_muiza.JPG
http://www.spoki.lv/izgudrojumi/Pasaule-apbrinojamakas-celtnes/156666