Kombinēta figūra - figūra, kas sastāv vismaz no divām figūrām.
Lai varētu aprēķināt kombinētas figūras laukumu, figūra ir jāsadala atsevišķās figūrās.
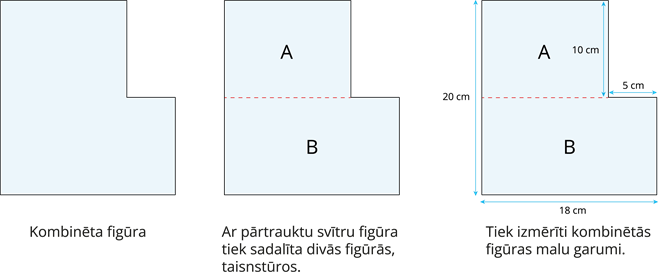
Kad kombinētā figūra ir sadalīta atsevišķās figūrās, šajā gadījumā taisnstūros, var sākt aprēķināt laukumu.
Vispirms ir jāaprēķina laukums, katrai figūrai, taisnstūrim atsevišķi.
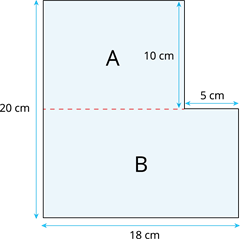
Sāksim ar \(A\) figūru. Šai figūrai laukumu aprēķina, sareizinot garumu ar platumu jeb \(S\) \(=\) \(a\) \(·\) \(b\)
Ir redzams, ka figūras platums ir \(10\) \(cm\), bet garums būs \(18\) \(cm\) \(-\) \(5\) \(cm\) \(=\) \(13\) \(cm\).
Tātad, \(S\) \(=\) \(10 · 13 = 130\) .
\(B\) figūra. Arī šai figūrai laukumu aprēķina, sareizinot garumu ar platumu jeb \(S\) \(=\) \(a\) \(·\) \(b\)
Ir redzams, ka platums būs \(10\) \(cm\), jo \(20\) \(cm\) \(-\) \(10\) \(cm\) \(=\) \(10\) \(cm\). Un garums ir \(18\) \(cm\).
Tātad, \(S\) \(=\) \(10 · 18 = 180\) .
Tagad visu figūru iegūtie laukumi ir jāsaskaita kopā.
Svarīgi!
Kombinētās figūras laukums \(=\) \(A\) figūras laukums \(+\) \(B\) figūras laukums.
Tātad, \(130\) \(+\) \(180\) \(=\) \(310\)
Vienlielas figūras ir tādas figūras, kuru laukums ir vienāds, bet to perimetrs un forma var būt dažādi.
Aplūko dažus piemērus!
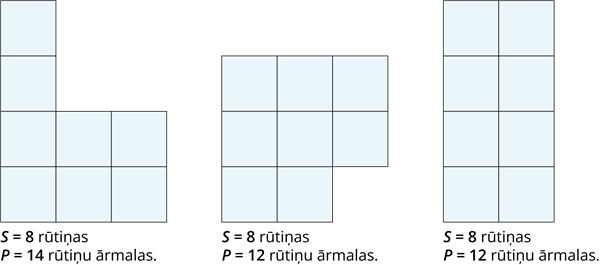
Attēlos ir redzamas trīs dažādas figūras, pēc formas.
Bet izskaitot rūtiņas ir redzams, ka šīs figūras ir vienlielas, jo tās ir noklātas ar \(8\) rūtiņām. Tātad laukumi ir vienādi!
Rēķinot perimetru, ir redzams, ka tas nav vienāds visām figūrām. Pārliecinies pats, izskaiti rūtiņu malu skaitu, skaitot pa ārmalu!
Vienlielas figūras var būt dažādas pēc formas un pēc perimetra, bet to laukumi ir vienādi!
Šeit Tu vari apskatīt vēl citu informāciju par vienlielām figūrām un to laukumu, un perimetru.
Izmēģini izveidot pats savas vienlielas figūras šeit .

