Telpas bāze — teorija. Matemātika, Augstskola: 1. kurss.

Par vektoru

\vec{a_{1}}, \vec{a_{2}}, ..., \vec{a_{n}}

lineāru kombināciju sauc izteiksmi

k_{1} \vec{a_{1}} + k_{2} \vec{a_{2}} + ... + k_{n} \vec{a_{n}}

, kur

k_{1}, k_{2}, ..., k_{n}

ir skaitļi.

Ja divi vektori

\vec{a}, \vec{b}

ir nekolineāri un ir atlikti no viena punkta, tad jebkuru citu iegūtās plaknes vektoru

\vec{c}

var izteikt kā šo divu vektoru lineāru kombināciju, turklāt vienā vienīgā veidā:

\vec{c} = k_{1} \vec{a} + k_{2} \vec{b}

. Tad vektorus

\vec{a}, \vec{b}

(secība ir svarīga) sauc par šīs plaknes bāzi, bet skaitļus

k_{1}, k_{2}

- par vektora

\vec{c}

koordinātām šajā bāzē.

(Šāda īpašība piemīt tikai nekolineāriem vektoriem.)

Vektorus sauc par komplanāriem, ja, tos atliekot no viena punkta, tie atrodas uz vienas plaknes.

Ja trīs vektori

\vec{a}, \vec{b}, \vec{c}

ir nekomplanāri, tad jebkuru citu vektoru

\vec{d}

var izteikt kā šo trīs vektoru lineāru kombināciju, turklāt vienā vienīgā veidā:

\vec{d} = k_{1} \vec{a} + k_{2} \vec{b} + k_{3} \vec{c}

. Tad vektorus

\vec{a}, \vec{b}, \vec{c}

(secība ir svarīga) sauc par telpas bāzi, bet skaitļus

k_{1}, k_{2}, k_{3}

- par vektora

\vec{d}

koordinātām šajā bāzē. (Šāda īpašība piemīt tikai nekomplanāriem vektoriem.)

Svarīgi!

Ja ir skaidrs, kāda ir plaknes vai telpas bāze, tad iepriekš aplūkotos vektorus var pierakstīt koordinātu formā:

\vec{c} = (k_{1}; k_{2})

vai

\vec{d} = (k_{1}; k_{2}; k_{3})

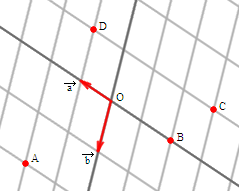
Piemērs:

Šai zīmējumā ir dota plakne, kuras bāze ir

\vec{a}, \vec{b}

. Un

\vec{AB} = - 4 \vec{a} - 2 \vec{b}

, tātad vektora

\vec{AB}

koordinātas šajā bāzē ir

(- 4; - 2)

- tas ir,

\vec{AB} = (- 4; - 2)

Citi piemēri ir

\vec{DA} = \vec{a} + 3 \vec{b} = (1; 3)

\vec{DC} = - 4 \vec{a} = (- 4; 0)

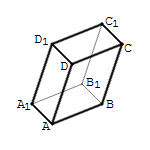
Piemērs:

Šeit savukārt ir dota telpa, par kuras bāzi var ņemt, piemēram,

\vec{A A_{1}}, \vec{AB}, \vec{AD}

. Tad

\vec{A C_{1}} = \vec{A A_{1}} + \vec{AB} + \vec{AD}

un tātad

\vec{A C_{1}} = (1; 1; 1)

Atradi kļūdu?

7. Telpas bāze