Svarīgi!
Tāpat kā lineārus algoritmus, arī cikliskos algoritmus var pierakstīt:
• vārdiski;
• grafiski (shematiski vai ar blokshēmu);
• ar programmu (skriptu).
• vārdiski;
• grafiski (shematiski vai ar blokshēmu);
• ar programmu (skriptu).
Piemērs:
Piemērs:

Trepēm katra pakāpiena platums un augstums ir 20 soļi. Izveidot algoritmu ar ciklu, lai zīmulis varētu uzzīmēt attēlotās trepes. Zīmēšana jāsāk vietā, kur atrodas zīmulis.
Cikliska algoritma vārdiskais pieraksts
Ja jāatkārto tikai viena darbība, tad atkārtošanas reižu skaitu var norādīt tajā pašā algoritma solī. Ja jāatkārto vairākas darbības, tad:
- pieraksta secīgi darbības;
- nākamajā solī pieraksta, kuras darbības un cik reizes jāatkārto.Piemērs:Piemēram:
1. Iet 20 soļus pa labi.
2. Iet 20 soļus uz leju.
3. Atkārtot 1. un 2. darbību vēl 4 reizes.
Lai uzzīmētu attēlā izveidotās trepes, faktiski darbības jāatkārto 5 reizes, bet tā kā 1. un 2. solī darbības vienu reizi jau ir izpildītas, tad pēc tam tās jāatkārto tikai 4 reizes.
Cikliska algoritma grafiskais pieraksts
Grafiski algoritmu var pierakstīt gan shematiski (ar zīmējumiem, shēmām, bultiņām u.c.), gan arī ar blokshēmu.
Grafiski algoritmu var pierakstīt gan shematiski (ar zīmējumiem, shēmām, bultiņām u.c.), gan arī ar blokshēmu.
Shematiskais pieraksts
Ja shematiski jāapraksta zīmējuma veidošana, visvienkāršāk to var pierakstīt ar bultiņām.
Iepriekš apskatītajā piemērā vienā virzienā jāiet vairāki soļi, tāpēc pirms algoritma uzrakstīšanas var paskaidrot, cik soļus katra bultiņa apzīmē. Piemēram:
Apzīmējumi:
•
•

Pieraksts ar blokshēmu
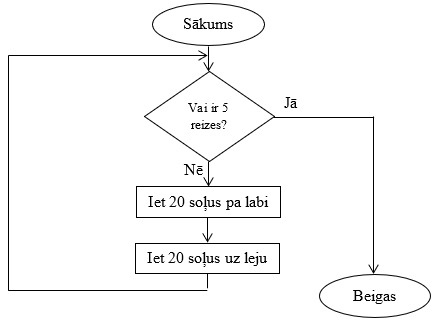
Veidojot blokshēmu cikliskam algoritmam, rūpīgi jāpārdomā, kāds nosacījums jāpārbauda pēc katras cikla darbību izpildes, lai zinātu, kura brīdī cikla darbība jābeidz.
Vienkāršoti aplūkotā piemēra algoritmu ar blokshēmu varētu attēlot šādi:
Veidojot blokshēmu cikliskam algoritmam, rūpīgi jāpārdomā, kāds nosacījums jāpārbauda pēc katras cikla darbību izpildes, lai zinātu, kura brīdī cikla darbība jābeidz.
Vienkāršoti aplūkotā piemēra algoritmu ar blokshēmu varētu attēlot šādi:
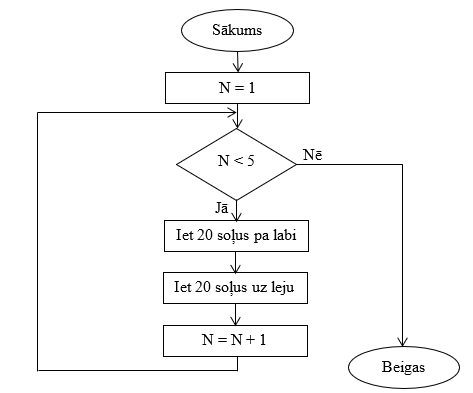
Tomēr cikla ar skaitītāju (zināms, cik reizes cikls jāizpilda) pieraksts ar blokshēmu ir sarežģītāks, jo tajā jāattēlo arī skaitītāja loma cikla izpildē. Attiecībā uz skaitītāju (blokshēmas piemērā – N ) nepieciešams norādīt trīs vērtības:
• sākuma vērtību – vērtību ar kādu uzsākt skaitīšanu. Visbiežāk tā ir 1, taču var būt arī jebkurš cits skaitlis, piemēram, elektroniskais pulkstenis stundu, minūšu un sekunžu skaitīšanu sāk no nulles;
• beigu vērtību – vērtība, kuru pārsniedzot cikls vairs nav jāatkārto;
• soli – vērtība par cik izmainās skaitītāja vērtība pēc atkārtojamo darbību izpildes. Arī šī vērtība visbiežāk ir 1.
• sākuma vērtību – vērtību ar kādu uzsākt skaitīšanu. Visbiežāk tā ir 1, taču var būt arī jebkurš cits skaitlis, piemēram, elektroniskais pulkstenis stundu, minūšu un sekunžu skaitīšanu sāk no nulles;
• beigu vērtību – vērtība, kuru pārsniedzot cikls vairs nav jāatkārto;
• soli – vērtība par cik izmainās skaitītāja vērtība pēc atkārtojamo darbību izpildes. Arī šī vērtība visbiežāk ir 1.

Blokshēmā vispirms skaitītājam N tiek piešķirta sākuma vērtība 1. Nosacījums, kas tiek pārbaudīts: vai N < 5. Pēc katras cikla darbību izpildes skaitītāja vērtība tiek palielināta par 1 (N=N+1) un atkal pārbaudīts nosacījums.
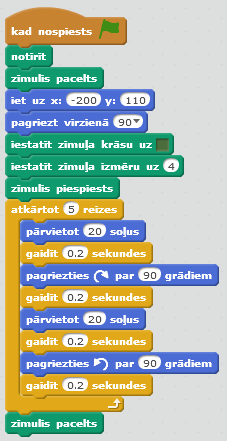
Algoritma pieraksts valodā Scratch
Atsauce:
https://datorika.startit.lv/datorika/klase/5/stunda/318