Uzdevumos par kustību ir jāprot izveidot pareizas sakarības starp lielumiem - ceļš, ātrums un laiks.
Lai aprēķinātu ceļu, ātrumu reizina ar ceļā pavadīto laiku.
Lai aprēķinātu laiku, veikto ceļu dala ar ātrumu.
Lai aprēķinātu ātrumu, veikto ceļu dala ar ceļā pavadīto laiku.
Ja izmanto pieņemtos apzīmējumus, ka \(s\) - ceļš, \(v\) - ātrums, \(t\) - laiks, var uzrakstīt formulas,
ceļš ,
laiks ,
ātrums .
Īpaši uzmanīgi jārisina uzdevumi par kustību vējā un straumē.
Vēja vai straumes ietekmē kustības ātrums izmainās.
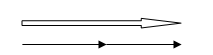
Ja laivai ir ātrums \(v\) un tā pārvietojas straumes virzienā, tad laivas un straumes ātrumi summējas.
Laivas kustības ātrums pa straumi vienāds ar .
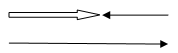
Ja laivai ir ātrums \(v\) un tā pārvietojas pret straumi, tad laivas ātrums kļūst mazāks.
Laivas kustības ātrums pret straumi vienāds ar .
Savstarpēji pretējo virzienu kustību ātrumi atšķiras par divkāršotu straumes ātrumu.
Piemēram, ja laivas ātrums pa straumi ir , bet ātrums pret straumi ir , tad laivas ātrums stāvošā ūdenī ir un straumes ātrums ir .
Pārbaude: laivas ātrums pa straumi un laivas ātrums pret straumi ir .
Ja kustību uzdevumā dots, ka pārvietošanās notiek ezerā, tad nav straumes, jo ezerā ir stāvošs ūdens.
Līdzīgi kustību ietekmē vējš. Vējš var ietekmēt lidojošu ķermeņu ātrumu un buru laivu ātrumu.
Ja objekts pārvietojas vēja virzienā, tad objekta un vēja ātrumi summējas.
Ja objekts pārvietojas pret vēju, tad tā ātrums kļūst mazāks par tik, cik ir vēja ātrums.