Skaitli, kas izsaka, par cik viens skaitlis lielāks nekā otrs, sauc par abu skaitļu starpību.
Skaitli, kurš izsaka, cik reižu viens skaitlis ir lielāks nekā otrs, sauc par abu skaitļu attiecību.
Piemēram, ja nogrieznis \(AB\) ir \(3\) reizes garāks par nogriezni \(MK\), tad nogriežņu \(AB\) un \(MK\) attiecība ir \(3\) jeb \(AB : MK = 3\).
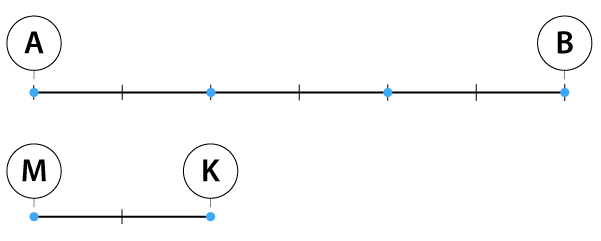
Attiecību var pierakstīt ar diviem skaitļiem.
Pieņemot īsākā nogriežņa (\(MK\)) garumu par \(1\) vienību, nogriežņa \(AB\) garums ir \(3\) tādas vienības.
Var uzrakstīt: \(AB:MK=3:1\).
To lasa: \(AB\) un \(MK\) attiecība ir \(3\) pret \(1\) jeb \(AB\) attiecas pret \(MK\) kā \(3\) pret \(1\).
Var rakstīt arī otrādi: \(MK:AB = 1:3\) (lasa - \(MK\) attiecas pret \(AB\) kā \(1\) pret \(3\)).
Par divu skaitļu attiecību sauc abu skaitļu dalījumu.
Piemēram, skaitļu \(20\) un \(4\) attiecība ir \(5\), jo \(20:4=5\). Tas izsaka, ka \(20\) ir \(5\) reizes lielāks nekā \(4\).
Dalījums \(20:4\) ir attiecības izteiksme, bet dalījums \(5\) ir attiecības vērtība.
Attiecības izteiksmi var vienkāršot, mazāko no skaitļiem pieņemot par \(1\) vienību*. Tad skaitļu attiecības izteiksmi \(20:4\) var aizstāt ar vienkāršāku attiecības izteiksmi \(5:1\) (\(5\) pret \(1\)).
Attiecības jēdzienu lieto skaitļu salīdzināšanai, lai noskaidrotu, cik reižu viens skaitlis ir lielāks par otru skaitli.
Ar attiecību var salīdzināt tikai viena un tā paša lieluma skaitliskās vērtības, piemēram, cik ir \(4\) m un \(20\) cm attiecība. Nevar aprēķināt, cik ir \(4\) kg un \(20\) cm attiecība, šādai salīdzināšanai nav jēgas.
Atceries!
Matemātikā mēs sastopamies ar šādiem lielumiem:
- garums,
- laukums,
- tilpums,
- masa,
- laiks,
- ātrums,
- temperatūra
Lielums ir īpašība, kas kopēja kādai objektu kopai, tā skaitliski dažādiem objektiem var būt atšķirīga.
Lai lielumus izmērītu, lieto atbilstošas mērvienības. Piemēram, garumu var mērīt metros, centimetros.
Izmantojot mērvienības, var izteikt lielumu skaitliskās vērtības jeb mēru.
Dažu lielumu, to mērvienību un skaitlisko vērtību piemēri
| Teikums | Lielums | Mērvienība | Skaitliskā vērtība (mērs) |
| Miltu masa bija \(2\) kg | masa | kilogrami | \(2\) kg |
| Kaķis gulēja \(6\) stundas | laiks | stundas | \(6\) h |
| Spainī ir \(10\) litri ūdens | tilpums | litri | \(10\) l |
* Pagaidām tiek aplūkotas tikai tādu skaitļu attiecības, kas izsakāmas ar naturālu skaitli, līdz ar to attiecības vienkāršotā izteiksmē viens loceklis vienmēr ir skaitlis \(1\).