Lai aprēķinātu taisnstūra laukumu, jāzina, no cik laukuma vienībām tas sastāv.
Laukuma vienības var būt, piemēram,
- kvadrātmilimetri,
- kvadrātcentimetri,
- kvadrātdecimetri
- kvadrātmetri
- kvadrātkilometri.
Cik ir dotā taisnstūra laukums, ja zināms, ka katras rūtiņas izmērs ir \(1\) ?
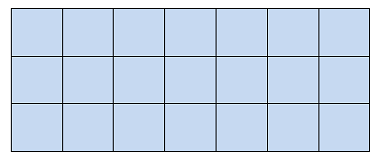
Var izskaitīt, cik kvadrātiņi veido taisnstūri. Skaitot pa vienam kvadrātiņam, iegūst \(21\) kvadrātiņu.
Tomēr izdevīgāk ir saskaitīt, cik kvadrātiņi veido taisnstūra garumu, cik - taisnstūra platumu, un abus skaitļus sareizināt.
Garums ir \(7\) kvadrātiņi, platums ir \(3\) kvadrātiņi, tātad kopā ir \(3·7=21\) kvadrātiņš, jeb dotā taisnstūra laukums ir \(S=\)\(21\) .
Lai noteiktu taisnstūra laukumu, pietiek uzzināt, cik vienības ir garums un platums.
Taisnstūra laukumu aprēķina, sareizinot garumu un platumu. Laukumu apzīmē ar burtu \(S\).
Nosaki dotā taisnstūra laukumu kvadrātmilimetros, ja zināms, ka katra mazā rūtiņa ir \(1\) .
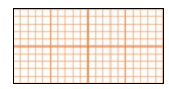
Redzam, ka būtu ļoti grūti saskaitīt visas mazās rūtiņas, bet var saskaitīt, ka garums ir \(20\) mm, platums ir \(10\) mm.
Tātad taisnstūra laukums ir \(S=\)\(20·10=200\)
Ja zināms, cik ir garums un platums, nav jāredz, no cik kvadrātvienībām sastāv taisnstūris, to var aprēķināt.
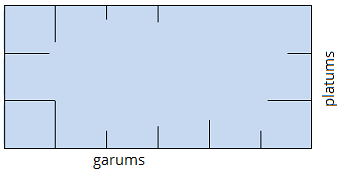
Taisnstūra laukums ir \(S=\)\(6·3=18\)
Nav svarīgi, kuru izmēru mēs uzskatām par garumu, kuru par platumu, galvenais izvēlēties dažādo malu garumus. Reizinātājus mainot vietām, reizinājums nemainās.
Piemēram, \(6·3=3·6=18.\)