Lai atrisinātu nevienādības \(|x|<a\) (vai \(\leq a\), \(\geq a\), \(> a\)), atbrīvojas no moduļa zīmes, balstoties moduļa ģeometriskajā interpretācijā.
Ko nozīmē moduļa ģeometriskā interpretācija?
Modulis ir skaitļa attālums līdz nullei (koordinātu ass sākumpunktam)
Piemēram, \(|x|<6\) nozīmē, ka uz koordinātu taisnes skaitlis \(x\) atrodas mazāk nekā \(6\) vienību attālumā no nulles, t.i., \(x\) atrodas starp \(-6\) un \(6\) (neieskaitot) jeb \(-6 < x < 6\).
Ja dots, ka \(|x|>4\), tad skaitlis \(x\) atrodas vairāk nekā \(4\) vienību attālumā no nulles, t.i., \(x<-4\) vai \(x>4\).
Vispārīgā gadījumā, ja \(a>0\):
Ja \(|x| < a\), tad uz koordinātu ass jāatrod tie punkti, kuru attālums līdz nullei ir mazāks nekā \(a\) vienības (\(a>0\)). 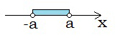 Tad \(-a < x < a \) jeb | Ja \(|x| > a\), tad uz koordinātu ass jāatrod tie punkti, kuri atrodas tālāk par \(a\) vienībām no nulles (\(a>0\)). 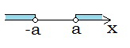 Tad \(x < -a\) vai \(x > a\). Uzmanies, neapvieno šīs nevienādības sistēmā! |