Riņķa līniju var ievilkt un to var apvilkt ap jebkuru trijstūri.
Trijstūrī ievilktas riņķa līnijas centrs ir bisektrišu krustpunkts.
Trijstūrim apvilktas riņķa līnijas centrs ir trijstūra malu vidusperpendikulu krustpunkts.
Regulāram trijstūrim ievilktas un apvilktas riņķa līnijas centrs ir bisektrišu, vidusperpendikulu, augstumu vai mediānu krustpunkts, jo visu šo līniju krustpunkti sakrīt.
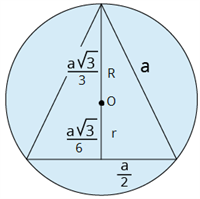
Vienādmalu trijstūrī ievilktas riņķa līnijas rādiuss
Ja regulārā trijstūrī ir ievilkta riņķa līnija, tad tās rādiuss (dots formulu lapā).
Var arī teikt, ka , kur \(h\) ir trijstūra augstums.
Ja dota trijstūra mala \(a\), tad (dots formulu lapā).
Apvilktas riņķa līnijas rādiuss
Ja regulāram trijstūrim ir apvilkta riņķa līnija, tad tās rādiuss, tad (dots formulu lapā).
Var arī teikt, ka , kur \(h\) ir trijstūra augstums.