Riņķa līniju var ievilkt un to var apvilkt ap jebkuru trijstūri.
Trijstūrī ievilktas riņķa līnijas centrs ir bisektrišu krustpunkts.
Trijstūrim apvilktas riņķa līnijas centrs ir trijstūra malu vidusperpendikulu krustpunkts.
Taisnleņķa trijstūrim apvilktas riņķa līnijas centrs atrodas hipotenūzas viduspunktā.

Taisnleņķa trijstūrim apvilktas riņķa līnijas rādiuss , kur \(c\) - hipotenūza.
Jebkurā trijstūrī, arī taisnleņķa trijstūrī ievilktās riņķa līnijas rādiuss ,
kur \(p\) - pusperimetrs, - laukums. Taisnleņķa trijstūra laukums , kur \(a\) un \(b\) ir katetes.
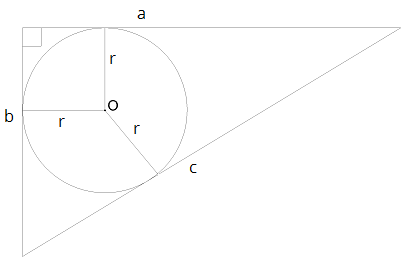
Ievēro! Matemātikas eksāmena formulu lapā \(r\) ir dots laukuma formulā, jāprot izteikt: