"Par centra leņķi sauc tādu leņķi, kura virsotne atrodas riņķa līnijas centrā, bet malas krusto riņķa līniju."
"Tāpat kā jebkurš leņķis plaknē, arī centra leņķis var būt šaurs, taisns, plats, izstiepts, atvērts vai pilns." (Jo pilns riņķis ir )
Centra leņķis vienāds ar tā loka leņķisko lielumu, uz kuru šis centra leņķis balstās.
Piemērs:
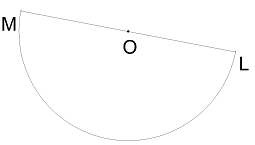
Dots: \(O\) - riņķa līnijas centrs, \(ML\) - diametrs.
Aprēķināt:
(centra leņķis, kas balstās uz diametru - loks jeb puse no riņķa)
"Par riņķa līnijā ievilktu leņķi sauc tādu leņķi, kura virsotne atrodas uz riņķa līnijas, bet malas krusto riņķa līniju."
"Ievilkts leņķis ir divas reizes mazāks nekā tam atbilstošais centra leņķis (nekā tā loka leņķiskais lielums, uz kura tas balstās)."
Piemērs:
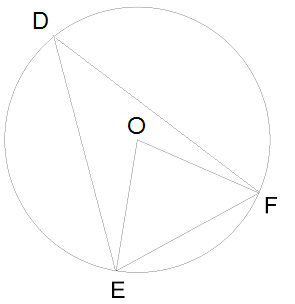
Dots:
\(O\) - riņķa līnijas centrs,
\(O\) - riņķa līnijas centrs,
loks
Aprēķināt:
un .
(kā centra leņķis, kas balstās uz lielu loku)
(ievilkts leņķis, balstās uz loku)