Trijstūris | Trijstūris | Trijstūris |
Trijstūris Bisektrises īpašība 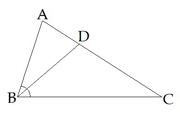 | Mediānu īpašība 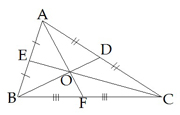 Viduslīnijas īpašība 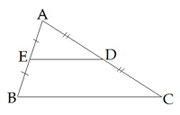 | |
Taisnleņķa trijstūris | Regulārs trijstūris | Līdzīgi trijstūri |
- augstums pret hipotenūzu , - katešu projekcijas uz hipotenūzas | ||
Paralelograms | Ievilkti un apvilkti četrstūri | Trapece |
Ievilkts četrstūris Apvilkts četrstūris |
Nogriežņi un leņķi, kas saistīti ar riņķa līniju | Regulāri \(n\)-stūri |
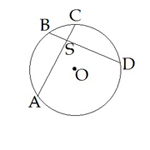 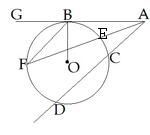 |
Prizma | Konuss | Riņķis un riņķa līnija |
Cilindrs | Nošķelts konuss | |
Piramīda | Lode un tās daļas | Vektori |
Nošķelta piramīda | - segmenta augstums |