Lai iegūtu funkcijas grafiku, funkcijas grafiku attēlo simetriski attiecībā pret asi tām vērtībām, kam .
Tām vērtībām, kurām , funkcijas grafiks sakrīt ar grafiku.
Vienkāršāk - tā grafika daļa, kas atrodas zem ass, attēlojas simetriski virs ass.
Piemērs:
Konstruē funkcijas grafiku.
Vispirms konstruē funkciju, kas atrodas moduļa zīmēs ,
tad sastāda tabulu:
0,25 | 0,5 | 1 | 2 | 4 | 8 | |
−2 | −1 | 0 | 1 | 2 | 3 |
Pamatgrafiks
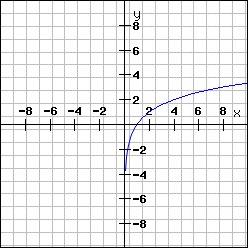
Negatīvo grafika daļu attēlo simetriski pret asi:
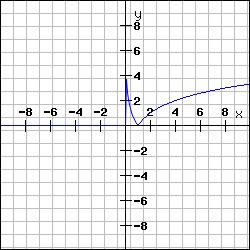
Ne vienmēr modulis izmaina pamatfunkcijas grafiku.
Piemērs:
Konstruē grafiku.
Pamatfunkcija:
1 | 0 | −1 | −2 | 3 | |
\(2\) | \(1\) | \(0,5\) | \(0,25\) | \(8\) |
Funkcijas grafiks sakrīt ar grafiku, jo tas ir pozitīvs visā definīcijas apgabalā.
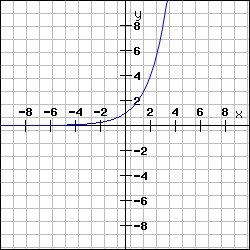
Piemērs:
Konstruē grafiku.
Pirmkārt, konstruē . Grafiks ir parabola, kam zari vērsti uz augšu (jo ).
Atrod virsotnes koordinātas:
Virsotne ir punktā .
Sastāda tabulu:
3 | 4 | 5 | |
2 | −1 | 6 |
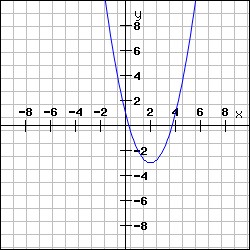
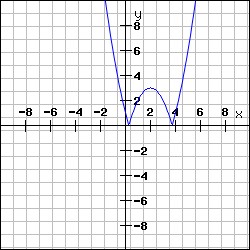
Grafiku konstruē vienā koordinātu plaknē. Šeit divi zīmējumi doti uzskatāmības dēļ.
Parabolu var konstruēt arī, atdalot binoma kvadrātu (skat. norādīto literatūras avotu).