Četrstūri, kura visas malas pieskaras riņķa līnijai, sauc par apvilktu četrstūri, bet riņķa līniju - par četrstūrī ievilktu riņķa līniju.
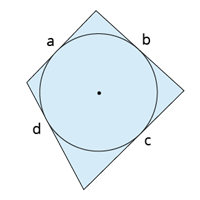
Ap riņķa līniju apvilkta četrstūra pretējo malu summas ir vienādas: \(a + c = b + d.\)
Pierādīsim šo apgalvojumu, izmantojot pieskaru nogriežņu vienādību.
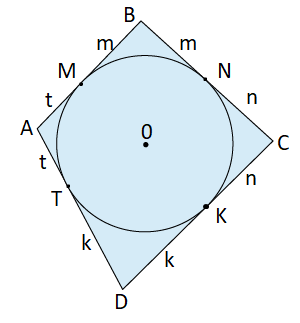
Dots: ABCD - ap riņķa līniju apvilkts četrstūris
Jāpierāda: AB+CD=AD+BC
Pierādījums
Pieņemsim, ka M, N, K un T ir punkti, kuros četrstūris pieskaras riņķa līnijai. No viena un tā paša punkta novilkto pieskaru garumi ir vienādi, tāpēc atbilstošos pieskaru nogriežņus apzīmēsim ar vienādiem burtiem.
MA=AT=t
MB=BN=m
NC=CK=n
KD=DT=k
Saskaitām pretējās malas, izmantojot pieņemtos apzīmējumus:
AB+CD=t+m+n+k
AD+BC=t+k+m+n
Redzam, ka AB+CD=AD+BC
Tas bija jāpierāda.
Piemērs:
Aprēķini apvilktas trapeces laukumu, ja tās sānu malas ir \(4\ cm\) un \(6\ cm\), bet ievilktās riņķa līnijas rādiuss ir \(2\ cm\).
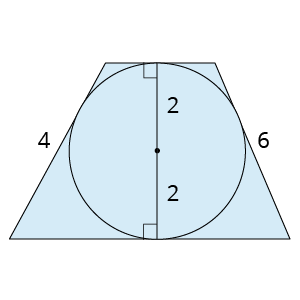
Risinājums:
Trapeces laukuma formula , kur \(a\) un \(b\) ir trapeces pamati, bet \(h\) - augstums.
Tā kā trapecē ir ievilkta riņķa līnija, tad sānu malu summa ir vienāda ar pamatu summu, tātad \(a + b = 4 + 6 = 10\ cm\).
Augstums ir divreiz garāks par rādiusu: \(h = 4\ cm\).
Tā kā trapecē ir ievilkta riņķa līnija, tad sānu malu summa ir vienāda ar pamatu summu, tātad \(a + b = 4 + 6 = 10\ cm\).
Augstums ir divreiz garāks par rādiusu: \(h = 4\ cm\).
Atbilde: Trapeces laukums ir \(20\ cm^2\).
Ne jebkurā četrstūrī var ievilkt riņķa līniju. Tikko pierādītajai teorēmai ir spēkā apgrieztā teorēma.
Ja četrstūra pretējo malu garumu summas ir vienādas, tad četrstūrī var ievilkt riņķa līniju.
Abas teorēmas var uzrakstīt sekojoši:
Riņķa līniju var ievilkt četrstūrī tad un tikai tad, ja tā pretējo malu summas ir vienādas.
Pārskats par četrstūriem, kuros var ievilkt riņķa līniju
Skaties atbilstošās formulas matemātikas eksāmena formulu lapā: formulas
Riņķa līnijai apvilkts kvadrāts
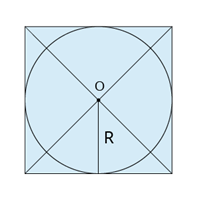
Centrs ir diagonāļu krustpunkts.
Rādiuss ir puse no kvadrāta malas.
Riņķa līnijai apvilkts rombs
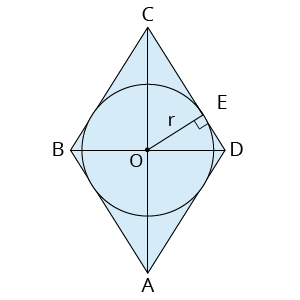
Centrs ir diagonāļu krustpunkts.
Rādiuss ir puse no romba augstuma.
Var lietot formulu: , kur \(S\) - romba laukums, \(p\) - pusperimetrs.
Riņķa līnijai apvilkta trapece, kurai pretējo malu summas ir vienādas.
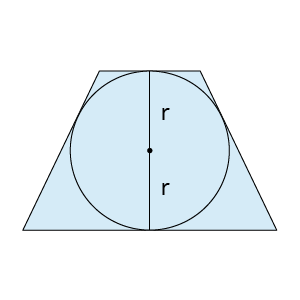
Centrs ir bisektrišu krustpunkts. 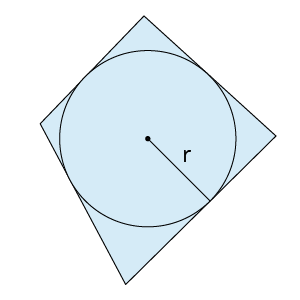
Rādiuss ir puse no augstuma. Ievēro, ka tā var nebūt vienādsānu trapece.
Riņķa līnijai apvilkts četrstūris, kuram pretējo malu summas ir vienādas

Centrs ir bisektrišu krustpunkts.
Formula , kur \(S\) - četrstūra laukums, \(p\) - pusperimetrs
Ap riņķa līniju apvilkta četrstūra laukumu aprēķina S = pr