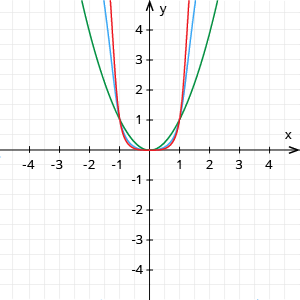
Funkciju, kuras vispārīgais veids ir , kur , sauc par pakāpes funkciju.
Ja \(n\) ir pozitīvs pāra skaitlis:
- Ja \(n=2\), tad iegūstam kvadrātfunkciju \(y=x^2,\) tās grafiks ir parabola, zīmējumā - zaļā krāsā.
- ja \(n=4\), tad \(y = x^4,\) zīmējumā - zilā krāsā;
- ja \(n=6\), tad \(y=x^6,\) zīmējumā - sarkanā krāsā;
- …
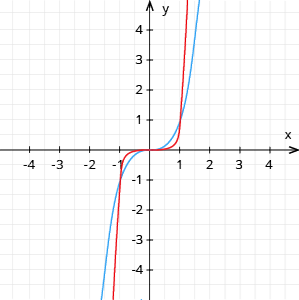
Ja \(n\) ir pozitīvs nepāra skaitlis:
- ja \(n = 1\), tad \(y = x\), lineāra funkcija, kas ir I un III kvadranta bisektrise;
- ja \(n=3\), tad \(y=x^3\), tās grafiks ir kubiskā parabola, zīmējumā - zilā krāsā;
- ja \(n=5\), tad \(y=n^5\), zīmējumā - sarkanā krāsā;
- …
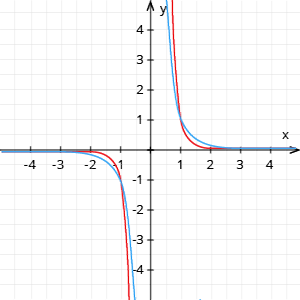
Ja \(n\) ir negatīvs nepāra skaitlis:
- ja \(n=-1\), tad \(y=x^{-1}\) jeb , tā ir apgrieztā proporcionalitāte, tās grafiks - hiperbola;
- ja \(n=-3\), tad , zīmējumā - zilā krāsā;
- ja \(n=-5\), tad , zīmējumā - sarkanā krāsā;
- ...
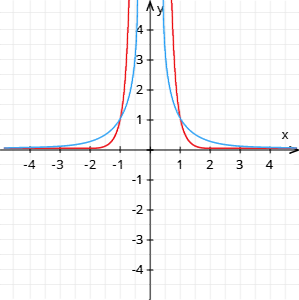
Ja \(n\) ir negatīvs pāra skaitlis:
- ja \(n=-2\), tad , grafiks ir hiperbola, kas novietojusies I un II kvadrantā, zīmējumā - zilā krāsā;
- ja \(n=-4\), tad , zīmējumā - sarkanā krāsā;
- ...