Funkciju , kur a ir pozitīvs reāls skaitlis (a > 0 ) un a nav vienāds ar 1, sauc par logaritmisko funkciju.
Definīcijas apgabals .
Vērtību apgabals E(y) = R (visi reālie skaitļi).
Lai konstruētu grafiku, sastāda vērtību tabulu, tajā izvēloties gan daļas, gan veselus skaitļus.
Piemērs:
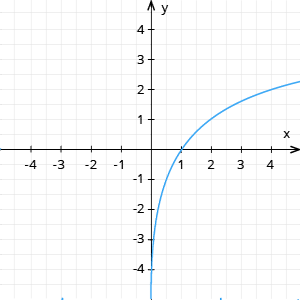
1. Konstruē grafiku funkcijai
x | 1 | 2 | 4 | ||
y | -2 | -1 | 0 | 1 | 2 |
...
Piemērs:
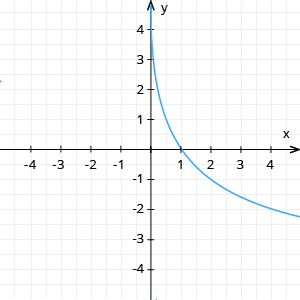
2. Konstruē grafiku funkcijai
x | 1 | 2 | 4 | ||
y | 2 | 1 | 0 | -1 | -2 |
...
Funkcija krusto Ox asi punktā (1;0), bet nekrusto Oy asi.
Svarīgi!
Funkcijas monotonitāte ir atkarīga no parametra a vērtības:
ja a > 1, funkcija aug (skat. 1. piem.)
ja 0 < a < 1, tad funkcija dilst (skat 2. piem.)
ja 0 < a < 1, tad funkcija dilst (skat 2. piem.)
Logaritmiskā funkcija nav periodiska, nav ne pāra, ne nepāra funkcija.
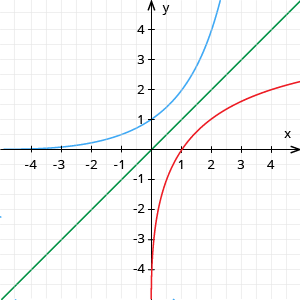
12. klasē uzzināsi, ka logaritmiskā funkcija un eksponentfunkcija ir savstarpēji inversas funkcijas, to grafiki ir simetriski pret taisni y = x
Piemērs:
Salīdzini un grafikus
un grafiki ir simetriski pret taisni y = x
Abas funkcijas ir augošas.
vērtību apgabals ir vienāds ar definīcijas apgabalu
definīcijas apgabals ir vienāds ar vērtību apgabalu, tas ir R