Rekursīva lielākā kopīgā dalītāja aprēķināšana
Izmantosim Eiklīda metodi, lai izveidotu rekursīvu funkciju LKD, kas aprēķina divu veselu skaitļu lielāko kopīgo dalītāju. Šīs metodes pamatā ir vienādība \(LKD(a,b) = LKD(a\ mod\ b)\) un arī \(LKD(a, 0) = a\).
\(a \ mod \ b\) ir mazāks par \(b\), tāpēc ar katru šīs vienādības izmantošanas reizi otrais skaitlis paliek aizvien mazāks un kādā brīdī kļūst vienāds ar 0. Ja \(b=0\), tad operācija \(a \ mod \ b\) rada kļūdu, tāpēc tādā gadījumā LKD ir skaitlis \(a\).
Šādi šī funkcija izskatās, uzrakstīta TurboPascal.
function LKD(a, b: integer): integer;
var atlikums: integer;
begin
if b=0
then LKD := a
else LKD := LKD(b, a mod b);
end;
Ja ir jāiegūst \(LKD(4,0)\) vērtība, tad viss ir skaidrs - otrais skaitlis (funkcijas arguments) ir nulle, un funkcijas vērtība ir pirmais skaitlis jeb \(4\).
Citos gadījumos ir sarežģītāk. Piemēram, ja jāiegūst \(LKD(1271, 369)\).
Tad \(LKD(1271, 369)\) izmanto \(LKD(369, 164)\) vērtību. \(LKD(369, 164)\) izmanto \(LKD(164, 41)\) vērtību. \(LKD(164,41)\) izmanto \(LKD(41,0)\) vērtību. Pie \(LKD(41,0)\) šis process apstājas, jo ir uzreiz zināma vērtība, kas ir 41.
Tad šī funkciju izsaukumu secība sāk sarukt. \(LKD(164,41)\) vērtība sanāk 41, tad \(LKD(369, 164)\) vērtība sanāk 41, tad \(LKD(369, 164)\) ir 41 un beigās arī \(LKD(1271, 369)\) ir 41.
Lūk ilustrācija tam, kā šajā gadījumā tiek izsauktas funkcijas.
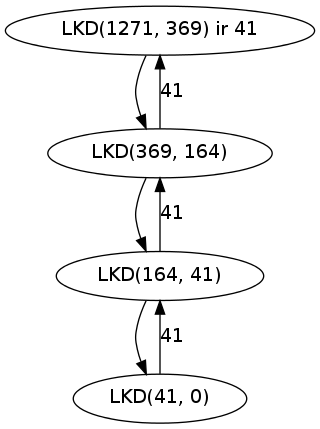
Un šeit ir maza programma ar šīs funkcijas pielietojumu.
program LKD;
function LKD(a, b: integer): integer;
begin
if b = 0 then LKD := a else LKD := LKD(b, a mod b);
end;
var a, b: integer;
begin
a := 1271;
b := 369;
writeln('Skaitlu ', a, ' un ', b, ' lielakais kopigais dalitajs ir ', LKD(a, b));
end.