Paralelograma laukums ir vienāds ar tā malas un augstuma, kurš novilkts pret taisni, kas satur šo malu, garumu reizinājumu:
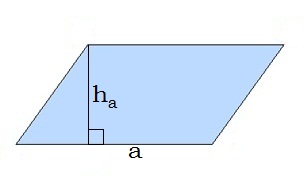
Par paralelograma augstumu sauc perpendikulu, kas savieno taisnes, kuras satur paralelograma divas pretējās malas.
Paralelogramā ir divi pāri paralēlu malu, tāpēc var novilkt divu dažāda garuma augstumus. Uzdevumu risināšanā parasti augstumu velk no virsotnes.
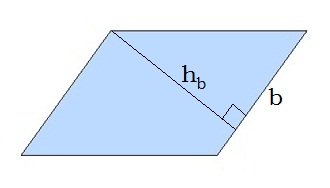
Šajā gadījumā
Izmantojot paralelograma laukuma formulas, var aprēķināt arī malu un augstumu garumus.
Piemērs:
Paralelograma malu garumi ir \(6\) cm un \(10\) cm, bet augstums pret īsāko malu ir \(8\) cm. Aprēķini tā augstuma garumu, kas vilkts pret garāko malu.
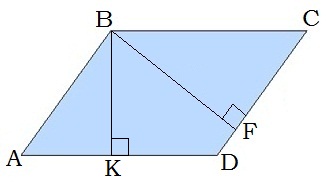
Dots:
\(DC = 6\) cm
\(BF = 8\) cm
\(AD = 10\) cm
Jāaprēķina:
\(BK\)
Risinājums:
Paralelograma \(ABCD\) laukumu var uzrakstīt divos veidos .
Neatkarīgi no tā, kuru laukuma izteiksmi izvēlas, paralelograma laukums ir viens un tas pats.
Atbilde: Augstums pret garāko malu ir \(4,8\) cm.

Dots:
\(DC = 6\) cm
\(BF = 8\) cm
\(AD = 10\) cm
Jāaprēķina:
\(BK\)
Risinājums:
Paralelograma \(ABCD\) laukumu var uzrakstīt divos veidos .
Neatkarīgi no tā, kuru laukuma izteiksmi izvēlas, paralelograma laukums ir viens un tas pats.
Atbilde: Augstums pret garāko malu ir \(4,8\) cm.