Aksiālā simetrija
"Divus punktus sauc par simetriskiem attiecībā pret taisni, ja nogrieznis, kas tos savieno, ir perpendikulārs pret šo taisni un taisne iet caur šī nogriežņa viduspunktu."
Šo taisni (t) sauc par simetrijas asi.
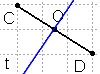 | CO = OD C un D - simetriski punkti pret taisni t |
"Figūras F1 un F2 sauc par simetriskām pret kādu taisni, ja katram figūras F1 punktam attiecībā pret šo taisni ir simetrisks punkts figūrā F2 un otrādi."
Aksiāli simetriskās figūrās atbilstošie figūru elementi ir vienādi. Aksiālajā simetrijā saglabājas attālumi.
Svarīgi!
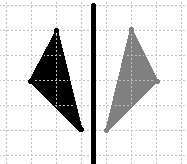
Aksiālā simetrija ir simetrija pret asi - spoguļattēls.
| 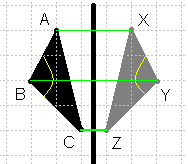 |
Piemērā:
1) nogrieznis attēlojas par tam vienādu nogriezni (AB = XY, BC = YZ, AC = XZ),
2) leņķis attēlojas par tam vienādu leņķi ,
Secinājums: figūra attēlojas par tai vienādu figūru .
Secinājums: figūra attēlojas par tai vienādu figūru .
Konstruēsim nogrieznim AB simetrisku nogriezni pret taisni t.
1) no katra punkta velk perpendikulus pret taisni t; 2) otrā pusē taisnei atliek vienādus nogriežņus;  | 3) savieno iegūtos punktus. Nogrieznis AB un ir aksiāli simetriski pret taisni t.  |