Saskaitīt divus naturālus skaitļus nozīmē aprēķināt, cik skaitīšanas vienību ir abos skaitļos kopā.
\(a+b=c \)
Vienādība \(4+6=10\) izsaka, ka skaitlī \(10\) ir tikpat vienu, cik pavisam vienu kopā ir skaitļos \(4\) un \(6\).
Darbības locekļu nosaukumi:
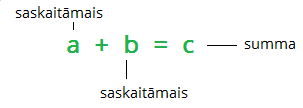 |
Saskaitīšanas pārvietojamības likums
Ja saskaitāmos pārvieto, tad summa nemainās.
\(a+b=b+a\)
\(4+6=6+4\)
Saskaitīšanas savienojamības likums
Ja saskaitāmos savieno grupās, summa nemainās.
\((a+b)+c=a+(b+c)\)
\((5+2)+8=5+(2+8)\)
Vieglāk ir saskaitīt \(5+(2+8)=5+10=15,\) nevis \((5+2)+8=7+8=15\).
Saskaitāmos drīkst pēc patikas pārvietot un savienot - ieslēgt iekavās vai iekavas atmest.
\(12+9+28+11=(12+28)+(9+11)=40+20=60\)
Atņemt no viena skaitļa otru nozīmē atrast tādu skaitli, kas summā ar otru skaitli dod pirmo skaitli
\(c-b=a\), jo \(a+b=c\)
Darbības locekļu nosaukumi:
 |
Saskaitīšana un atņemšana ir savstarpēji pretējas darbības.
\(2+5=7\)
\(5+2=7\)
\(7-2=5\)
\(7-5=2\)
Tādus trīs skaitļus \(2\), \(5\), \(7\), kādi aplūkoti piemērā, var saukt par savstarpēji draudzīgiem skaitļiem.