Nogriezni, kurš nav perpendikulārs plaknei un kura viens galapunkts atrodas plaknē, sauc par slīpni pret plakni.
Slīpnes punktu, kas atrodas plaknē sauc par slīpnes pamatu.
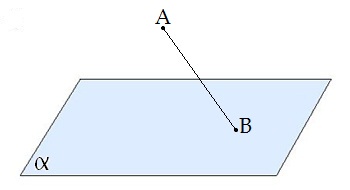
Slīpne ir nogrieznis .
Slīpnes pamats ir .
Ja no punkta ārpus plaknes novelk plaknei perpendikulāru taisni, tad šīs taisnes nogriezni no minētā punkta līdz plaknei sauc par perpendikulu, kas novilkts no punkta pret plakni.
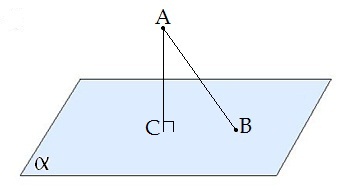
Perpendikuls ir nogrieznis .
Perpendikula garumu no punkta līdz plaknei sauc par attālumu no punkta līdz plaknei.
Ja no punkta, kas atrodas ārpus plaknes, novelk gan perpendikulu, gan slīpni, tad nogriezni, kas savieno perpendikula un slīpnes galapunktus plaknē, sauc par slīpnes projekciju.
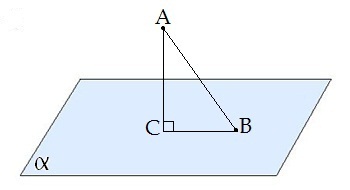
Slīpnes projekcija ir nogrieznis .
Trijstūris ir taisnleņķa trijstūris.
Par slīpnes leņķi ar plakni sauc leņķi starp slīpni un tās projekciju plaknē.
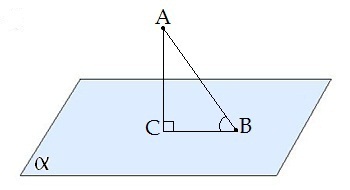
Leņķis, ko veido slīpne ar plakni, ir .
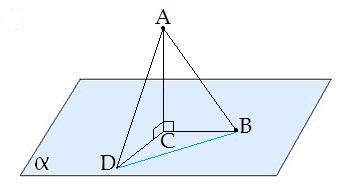

No divām slīpnēm, kas vilktas no viena punkta, garākā projekcija ir garākajai slīpnei.
Ja , tad .
ir leņķis starp slīpnēm.
ir leņķis starp projekcijām.
Nogrieznis ir attālums starp slīpņu pamatiem.