Lineāra funkcija
Analītiskā izteiksme: , kur un ir reāli skaitļi.
Lineāras funkcijas grafiks ir taisne.
Definīcijas apgabals ir visi reālie skaitļi.
Vērtību apgabals ir visi reālie skaitļi.
Parametrs ir taisnes virziena koeficients:
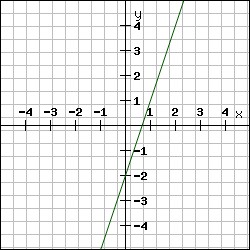
- ja , tad funkcija ir augoša (skat. 1. piem.)
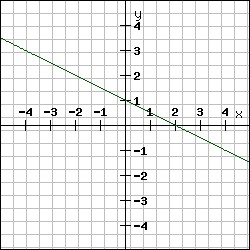
- ja , tad funkcija ir dilstoša (skat. 2. piem.)
Parametrs norāda, kurā punktā taisne krusto y asi.
Vienādojuma atrisinājums ir funkcijas sakne (krustpunkts ar asi).
1. piemērs:
Funkcijas sakne ir
2. piemērs:
Funkcijas sakne ir