Tādas nevienādības, kurās nezināmais ir trigonometriskās funkcijas arguments (leņķis), sauc par trigonometriskām nevienādībām.
Vidusskolas kursā ir jāprot risināt pamatnevienādības:
\(\sin x<a\); \(\cos x< a\), \(\operatorname{tg}x<a\), \(\operatorname{ctg}x<a\)
Risinājumā izmanto vienības riņķi.
Īsa risinājuma gaita:
- Uzzīmē vienības riņķi, atrod dotās funkcijas asi.
- Uz atbilstošās ass atliek doto skaitlisko (\(a\)) vērtību.
- Ņemot vērā nevienādības zīmi, iekrāso atbilstošo loka daļu.
- Nosaka pagrieziena leņķa vērtības (bieži vien tās vajag atrisināt no atbilstošā vienādojuma un tad atlikt riņķī).
- Nolasa atbilstošo intervālu, ņemot vērā, ka leņķi pieaug pretēji pulksteņa rādītāju virzienam.
Piemērs:
Atrisini nevienādību
1. Uz \(y\) ass atliek punktu un caur šo punktu paralēli \(x\) asij novelk taisni. Uz vienības riņķa līnijas iegūst punktus, kas atbilst leņķiem un .
2. Tā kā , tad uz \(y\) ass iezīmējam to daļu, kurai atbilst skaitļi, kas lielāki par ,
tātad - uz augšu no punkta \(y=\frac{1}{2}\).
3. Iezīmē to riņķa līnijas daļu, kurai atbilstošo punktu ordinātas (\(y\)) ir lielākas nekā .
Nevienādības atrisinājumam atbilst sarkanās krāsas loka punkti.
4. Lai pareizi uzrakstītu atbildes intervālu, jāatceras, ka pa iezīmēto loku pārvietojas pretēji pulksteņa rādītāju virzienam.
Tā kā sinusa funkcijas periods ir , tad, pieskaitot iegūtajām leņķa vērtībām perioda daudzkārtni , iegūst nevienādības visus atrisinājumus:
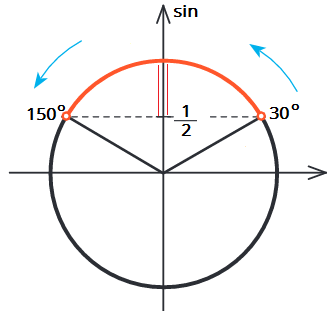
Lai zīmējumā pareizi atliktu leņķus, atrisina vienādojumu
Atbilde: