Lai atrisinātu nevienādības, kas satur izteiksmes ar moduļiem, vispirms atbrīvojas no moduļa zīmes, t.i., uzraksta atbilstošās ekvivalentās nevienādības bez moduļa zīmēm.
Divas nevienādības sauc par ekvivalentām, jo to atrisinājumu kopas ir vienādas.
Ekvivalence tulkojumā nozīmē līdzvērtīgs, ar vienādu nozīmi.
Nevienādība \(|f(x)| < a\), ja \(a > 0\), ir ekvivalenta ar divkāršu nevienādību , t.i., ar nevienādību sistēmu
Piemērs:
Atrisini nevienādību \( |x-3| < 5\).
Atbilde ir intervālu šķēlums.
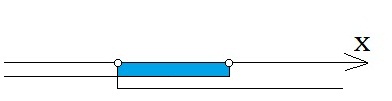
Atbilde:
Atbilde ir intervālu šķēlums.

Atbilde:
Nevienādība \(|f(x)| > a\), kur , ir ekvivalenta ar divu nevienādību apvienojumu: \(f(x) > a\) vai \(f(x)< -a\). Ievēro, tā nav nevienādību sistēma, jo abas nevienādības nevar izpildīties vienlaicīgi!
Piemērs:
Atrisini nevienādību \(|x-3| > 5\).
\(x - 3 > 5\) vai \(x - 3 < -5\)
\(x > 8\) vai \(x < -2\)
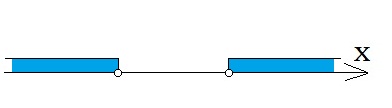
Atbilde ir intervālu apvienojums
Atbilde:
\(x - 3 > 5\) vai \(x - 3 < -5\)
\(x > 8\) vai \(x < -2\)

Atbilde ir intervālu apvienojums
Atbilde: