Četrstūri, kura visas virsotnes atrodas uz riņķa līnijas, sauc par ievilktu četrstūri, bet riņķa līniju - par četrstūrim apvilktu riņķa līniju.
Piemērs:
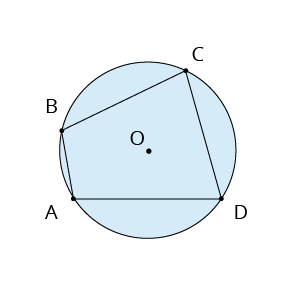
Ievilkta četrstūra vienas malas pieleņķi ir \(60°\) un \(70°\).
Aprēķini pārējos četrstūra leņķus!
Dots:
\(\sphericalangle B = 60°\)
\(\sphericalangle C = 70°\)
Jāaprēķina:
\(\sphericalangle D\); \(\sphericalangle A\)
Risinājums:
\(\sphericalangle B + \sphericalangle D = 180°\)
\(\sphericalangle C + \sphericalangle A = 180°\)
\(\sphericalangle D = 180° - 60° = 120°\)
\(\sphericalangle A = 180° - 70° = 110°\)
Riņķa līniju ap četrstūri var apvilkt tad un tikai tad, ja tā pretējo leņķu summa ir \(180°\).
Pārskats par četrstūriem, ap kuriem var apvilkt riņķa līniju
1) Riņķa līnijā ievilkts kvadrāts
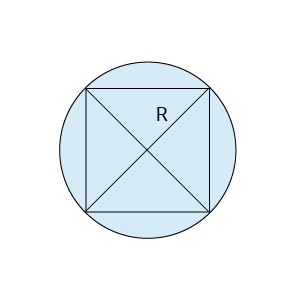
Centrs ir diagonāļu krustpunkts.
Apvilktas riņķa līnijas rādiuss ir puse no diagonāles garuma.
Ja kvadrāta mala ir , tad diagonāle ir , bet .
2) Riņķa līnijā ievilkts taisnstūris
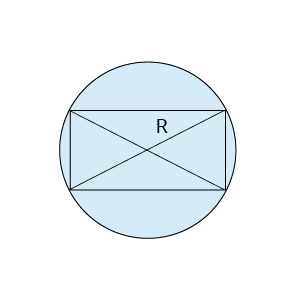
Apvilktas riņķa līnijas centrs ir diagonāļu krustpunkts.
Apvilktas riņķa līnijas rādiuss ir puse no diagonāles garuma.
Diagonāles garumu rēķina, piemēram, ar Pitagora teorēmu, ar sakarībām taisnleņķa trijstūrī.
3) Riņķa līnijā ievilkta vienādsānu trapece
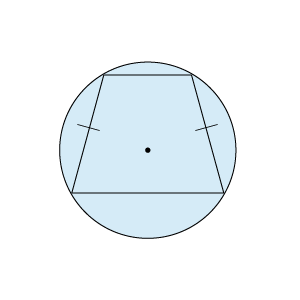
Apvilktas riņķa līnijas centrs ir malu vidusperpendikulu krustpunktā.
R.l. centrs var būt trapeces iekšpusē, ārpusē vai garākā pamata vidū.
Apvilktas riņķa līnijas rādiusa aprēķināšanai var izmantot trijstūrim apvilktas riņķa līnijas R formulu:
4) Riņķa līnijā ievilkts patvaļīgs četrstūris, kura pretējo leņķu summa ir \(180°\)
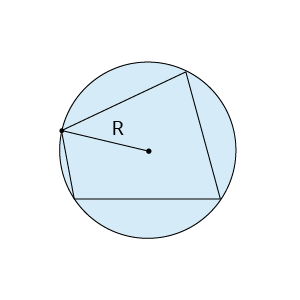
Apvilktas riņķa līnijas centrs ir malu vidusperpendikulu krustpunktā.