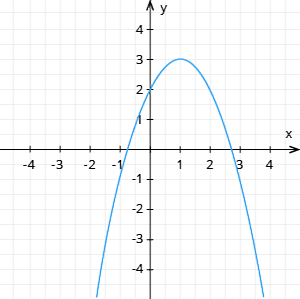
Funkcijai \(y = f(x)\) punktā ir lielākā vērtība, ja visiem \(x\) ir spēkā nevienādība \(f(x)<f(x_0)\) jeb visas funkcijas vērtības ir mazākas par \(f(x_0)\).
1. zīmējumā dotajai funkcijai lielākā vērtība ir \(f(1) = 3\).
Funkcijai \(y = f(x)\) punktā ir mazākā vērtība, ja visiem \(x\) ir spēkā nevienādība \(f(x)>f(x_0)\) jeb visas funkcijas vērtības ir lielākas par \(f(x_0)\).
2. zīmējumā dotajai funkcijai mazākā vērtība ir \(f(1) = -2\).
 1. zīm. | 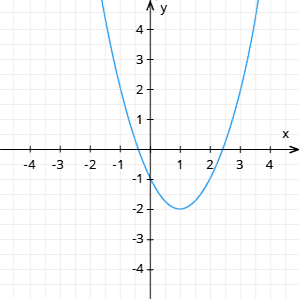 2. zīm. |
Vislielāko vai vismazāko vērtību visā tās definīcijas apgabalā funkcija sasniedz punktā, kurā mainās dilšanas un augšanas intervāli.
Svarīgi!
Kvadrātfunkcija savu lielāko vai mazāko vērtību sasniedz punktā, kas ir parabolas virsotne.
Risinot uzdevumus, bieži vien nav svarīgi konstruēt pašas funkcijas grafiku, bet pietiek ar to, ka aprēķina, kāda ir funkcijas lielākā vai mazākā vērtība.
Piemērs:
Gaisā izšāva raķeti. Raķetes attālumu no zemes virsmas (metros) laika momentā \(t\) var aprēķināt ar formulu \(h(t)= 60t -t^2\). Kāds būs maksimālais attālums no zemes virsmas?
Risinājums:
Nav vajadzības konstruēt kvadrātfunkciju, pietiek zināt, ka parabolai zari ir uz leju un tai eksistē lielākā vērtība.
Aprēķina parabolas virsotnes \(x\) koordinātu:
\(x_0\) šajā piemērā nozīmē - pēc cik sekundēm raķete sasniegs savu augstāko punktu (jo funkcijas arguments ir laiks).
Virsotnes \(y\) koordināta ir metri.
Tā kā funkcijas vērtības ir sasniegtais augstums, tad \(y_0\) nozīmē maksimālo augstumu.
Atbilde:
Maksimālais attālums no zemes virsmas būs \(900\) metri.
Maksimālais attālums no zemes virsmas būs \(900\) metri.