"Par trijstūra augstumu sauc perpendikulu, kas novilkts no trijstūra virsotnes pret taisni, kas satur pretējo trijstūra malu."
"Perpendikuls no punkta B pret taisni AC ir īsākais no attālumiem, kas savieno punktu B ar taisni AC."
Perpendikuls veido taisnu leņķi. Zīmējumā taisnu leņķi apzīmē ar nelielu kvadrātu.


BD ir augstums, kas vilkts pret malu AC
Augstumi var:
atrasties trijstūra iekšpusē (šaurleņķu ABC),
atrasties trijstūra ārpusē (platleņķa GHI),
sakrist ar trijstūra malu (taisnleņķa MNO).
atrasties trijstūra ārpusē (platleņķa GHI),
sakrist ar trijstūra malu (taisnleņķa MNO).

NP - augstums, jo NPMO.
MN - augstums, jo MNNO.
ON - augstums, jo ONMN.
MN - augstums, jo MNNO.
ON - augstums, jo ONMN.
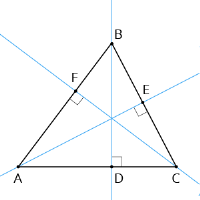
BD - augstums, jo BDAC.
CF - augstums, jo CFAB.
AE - augstums, jo AEBC.
CF - augstums, jo CFAB.
AE - augstums, jo AEBC.

Platleņķa trijstūrī augstumi, kas vilkti no šauro leņķu virsotnēm, atrodas ārpus trijstūra (uz trijstūra malu pagarinājumiem).