Vektors un tā garums
Orientēts nogrieznis ir nogrieznis, kas vērsts no fiksēta sākuma punkta uz beigu punktu.
To apzīmē ar , kur ir sākuma punkts un ir beigu punkts.

Ja divus orientētus nogriežņus un var, izmantojot paralēlo pārnesi, pārvietot tā, ka tie sakrīt (t.i., tiem sakrīt sākuma punkti un sakrīt beigu punkti), tad saka, ka tie atbilst vienam un tam pašam vektoram, un raksta . Tad saka arī, ka vektori un ir vienādi.
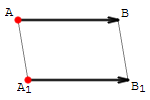
Divi vektori ir vienādi tad un tikai tad, ja:
1) atbilstošie orientētie nogriežņi atrodas uz paralēlām taisnēm vai uz vienas taisnes;
2) tie ir vienādi gari;
3) tie ir pareizi orientēti (var panākt, ka vienlaikus sakrīt sākuma punkti un sakrīt beigu punkti).
1) atbilstošie orientētie nogriežņi atrodas uz paralēlām taisnēm vai uz vienas taisnes;
2) tie ir vienādi gari;
3) tie ir pareizi orientēti (var panākt, ka vienlaikus sakrīt sākuma punkti un sakrīt beigu punkti).
Ja nofiksē vektora sākuma punktu (un iegūst konkrētu orientēto nogriezni), tad to sauc par vektora atlikšanu no šī punkta. Un attiecīgo orientēto nogriezni - par vektoru, kas atlikts no attiecīgā punkta.
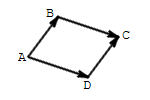
Piemērs:
1) Ja ir paralelograms, tad un .
2) un ir vienādi vektori, kas atlikti no dažādiem punktiem - no un .
Svarīgi!
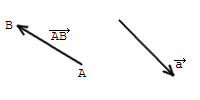
Vektoru var apzīmēt divos veidos:
1) - vispirms norādot punktu, no kura tas atlikts (), un tad attiecīgo beigu punktu ();
2) - ar mazo latīņu alfabēta burtu (taču literatūrā bieži bultiņas vietā izmanto burta paresnināšanu - ).
1) - vispirms norādot punktu, no kura tas atlikts (), un tad attiecīgo beigu punktu ();
2) - ar mazo latīņu alfabēta burtu (taču literatūrā bieži bultiņas vietā izmanto burta paresnināšanu - ).
Ja vektora beigu punkts sakrīt ar tā sākuma punktu, tad to sauc par nulles vektoru.
Nulles vektoru apzīmē ar . Vektoru, kas nav nulles vektors, sauc par nenulles vektoru.
Par vektora garumu (jeb moduli) sauc tam atbilstošā nogriežņa garumu.
1) Vienādiem vektoriem ir vienāds garums - tiem atbilstošos nogriežņus var iegūt vienu no otra ar paralēlo pārnesi un tātad to garumi ir vienādi.
2) Nulles vektora garums ir , jo atbilstošajam nogrieznim abi gali sakrīt un tad, protams, tā garums ir .