Funkcijas atvasinājums — teorija. Matemātika, Augstskola: 1. kurss.

Funkcijas atvasinājums

Funkcijas pieauguma un argumenta pieauguma attiecības robežu, kad argumenta pieaugums tiecas uz nulli, sauc par funkcijas atvasinājumu.

Funkcijas

y = f (x)

atvasinājumu apzīmē ar vienu no simboliem:

y^{'}, f^{'} (x), \frac{dy}{dx}, \frac{d}{dx} f (x) .

Funkcijas atvasinājuma atrašanu sauc par funkcijas atvasināšanu vai diferencēšanu.

Svarīgi!

Lai noteiktu funkcijas atvasinājumu:

1) nosaka argumenta pieaugumam $Δ x$ atbilstošo funkcijas pieaugumu

$Δ y = f (x + Δ x) - f (x)$ ;

2) sastāda funkcijas pieauguma un argumenta pieauguma attiecību $\frac{Δ y}{Δ x}$ un vienkāršo to;

3) aprēķina šīs attiecības robežu, kad $Δ x \to 0$ .

Kāpēc lieto atvasinājumu?

Pieņemsim, ka materiāls punkts kustas nevienmērīgi pa taisni. Tad, izvēloties kustības taisni par koordinātu asi, punkta stāvokli katrā laika momentā t raksturo punkta koordināta $x$ ( skat. zīm.).

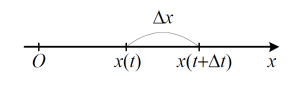
Funkciju $x = x(t)$, kas izsaka materiāla punkta koordinātas $x$ atkarību no laika $t$, sauc par materiāla punkta kustības likumu. Pieņemsim, ka laikā

Δ t

materiāls punkts veic ceļu

Δ x

, t.i. laika momentā

t + Δ t

punkta koordināta ir

x (t) + Δ x = x (t + Δ t)

. Tad punkta vidējo ātrumu var aptuveni aprēķināt pēc formulas

$v_{vid} = \frac{Δ x}{Δ t} = \frac{x (t + Δ t) - x (t)}{Δ t}$ .

Punkta momentāno ātrumu iegūsim, samazinot laiku $Δ t$ līdz nullei, t.i., aprēķinot robežu, kad $Δ t \to 0$ . Tātad materiāla punkta momentānais ātrums ir

v_{mom} = \lim_{Δ t \to 0} \frac{Δ x}{Δ t} = \lim_{Δ t \to 0} \frac{x (t + Δ t) - x (t)}{Δ t}

Faktiski šī formula arī definē funkcijas atvasinājumu. Taču to nodefinēsim patvaļīgai funkcijai

y = f (x)

. Pieņemsim, ka šī funkcija ir definēta kādā punktā x un tā apkārtnē. Izmainīsim x par

Δ x

. Tad funkcija mainās par

Δ y = f (x + Δ x) - f (x)

. Sastādīsim attiecību

\frac{Δ y}{Δ x} = \frac{f (x + Δ x) - f (x)}{Δ x} .

Šo attiecību sauc par funkcijas maiņas vidējo ātrumu intervālā

[x; x + Δ x]

un tā izsaka funkcijas izmaiņu, kas aprēķināta vienai argumenta izmaiņas vienībai.

Piemērs:

Noteikt funkcijas

y = x^{3}

atvasinājumu!

1) noteiksim argumenta pieaugumam

Δ x

atbilstošo funkcijas pieaugumu:

Δ y = {(x + Δ x)}^{3} - x^{3} = x^{3} + 3 x^{2} Δ x + 3 x {(Δ x)}^{2} + {(Δ x)}^{3} - x^{3} = 3 x^{2} Δ x + 3 x {(Δ x)}^{2} + {(Δ x)}^{3}

2) noteiksim funkcijas pieauguma un argumenta pieauguma attiecību:

\frac{Δ y}{Δ x} = \frac{3 x^{2} Δ x + 3 x {(Δ x)}^{2} + {(Δ x)}^{3}}{Δ x} = \frac{Δ x (3 x^{2} + 3 x Δ x + {(Δ x)}^{2})}{Δ x} = 3 x^{2} + 3 x Δ x + {(Δ x)}^{2}

3) aprēķināsim iegūtās attiecības robežu, kad Δx →0 :

$y^{'} = \lim_{Δ x \to 0} \frac{Δ y}{Δ x} = \lim_{Δ x \to 0} (3 x^{2} + 3 x Δ x + {(Δ x)}^{2}) = 3 x^{2} + 3 x \cdot 0 + 0^{2} = 3 x^{2}$

Tātad

${(x^{3})}^{'} = 3 x^{2}$

Parasti funkcijas neatvasina pēc definīcijas, jo tas ir sarežģīts un laikietilpīgs process. To dara, izmantojot atvasināšanas formulas:

$\begin{array}{l} 1 . {(C)}^{'} = 0, kur C = const \\ 2 . {(\ln x)}^{'} = \frac{1}{x} \\ 3 . {(\log_{α} x)}^{'} = \frac{1}{x lna} \\ 4 . {(a^{x})}^{'} = a^{x} lna \\ 5 . {(e^{x})}^{'} = e^{x} \\ 6 . {(x^{α})}^{'} = α x^{α - 1} \\ 7 . {(\sin x)}^{'} = \cos x \\ 8 . {(\cos x)}^{'} = - \sin x \\ 9 . {(tg x)}^{'} = \frac{1}{\cos^{2} x} \\ 10 . {(ctg x)}^{'} = - \frac{1}{\sin^{2} x} \\ 11 . {(\arcsin x)}^{'} = \frac{1}{\sqrt{1 - x^{2}}} \\ 12 . {(\arccos x)}^{'} = - \frac{1}{\sqrt{1 - x^{2}}} \\ 13 . {(arctg x)}^{'} = \frac{1}{1 + x^{2}} \\ 14 . {(arcctg x)}^{'} = - \frac{1}{1 + x^{2}} \\ 15 . {(sh x)}^{'} = ch x \\ 16 . {(ch x)}^{'} = sh x \\ 17 . {(th x)}^{'} = \frac{1}{{ch}^{2} x} \\ 18 . {(cth x)}^{'} = - \frac{1}{{sh}^{2} x} \end{array}$

Iepriekšējā tēma

Atgriezties tēmā

Nākamā teorija

Nosūtīt atsauksmi

Atradi kļūdu?

Sūti mums ziņu!

1. Funkcijas atvasinājums

Teorija