Attālums no taisnes līdz punktam, normālvienādojums — teorija. Matemātika, Augstskola: 1. kurss.

Punkta Attālums līdz taisnei. Taisnes normālvienādojums.

Svarīgi!

Punkta

M_{0} (x_{0}; y_{0})

attālums līdz taisnei

Ax + Bx + C = 0

ir vienāds ar izteiksmes

\frac{|A x_{0} + B y_{0} + C|}{\sqrt{A^{2} + B^{2}}}

vērtību.

\begin{array}{l} |\vec{O M_{0}}| = |\cos α| \cdot |\vec{OM}| = \\ = \frac{|\vec{OM} \cdot \vec{n}|}{|\vec{OM}| \cdot |\vec{n}|} \cdot |\vec{OM}| = \\ = \frac{|\vec{OM} \cdot \vec{n}|}{|\vec{n}|} = \\ = \frac{|(\vec{r_{M}} - \vec{r_{O}}) \cdot \vec{n}|}{|\vec{n}|} = \\ = \frac{|\vec{r_{M}} \cdot \vec{n} - \vec{r_{O}} \cdot \vec{n}|}{|\vec{n}|} = \\ = \frac{|- C - A x_{0} - B y_{0}|}{\sqrt{A^{2} + B^{2}}} = \\ = \frac{|A x_{0} + B y_{0} + C|}{\sqrt{A^{2} + B^{2}}} \end{array}

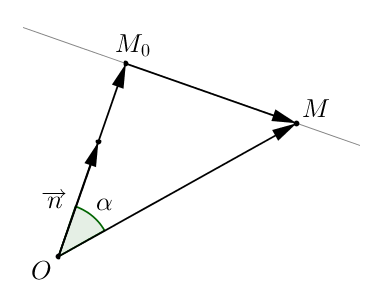
Šādi tiek iegūta izteiksme, ar ko aprēķina punkta attālumu līdz taisnei.

Te tika izmantots tas, ka taisnes normālvektora

\vec{n} = (A; B)

un jebkura taisnes punkta rādiusvektora

\vec{r}

skalārais reizinājums ir vienāds ar

- C

(kur C ir koeficients no attiecīgā taisnes vispārīgā vienādojuma).

Ja jāaprēķina taisnes attālums no koordinātu sākumpunkta, tad

(x_{0}; y_{0}) = (0; 0)

un attiecīgā izteiksme kļūst vienkāršāka:

\frac{|C|}{\sqrt{A^{2} + B^{2}}}

Vienādojumu, ko iegūst, izdalot taisnes vispārīgo vienādojumu ar

\pm \sqrt{A^{2} + B^{2}}

(zīme jāņem pretēja koeficienta C zīmei), sauc par taisnes normālvienādojumu.
Tad tiek iegūts vienādojums

x \cos α + y \sin α - p

, kur

α

ir leņķis starp taisni un Ox ass pozitīvo virzienu, bet p ir attālums no taisnes līdz koordinātu sākumpunktam.

Atradi kļūdu?

9. Attālums no taisnes līdz punktam, normālvienādojums