No punkta novilktas riņķa līnijas pieskares 2 — teorija. Matemātika, Augstskola: 1. kurss.

No punkta novilktu pieskaru pieskaršanās punktu noteikšana

Svarīgi!

Ja riņķa līnijas rādiuss ir r, bet punkta attālums līdz riņķa līnijas centram ir l, un no punkta ir novilktas pieskares šai riņķa līnijai, tad pieskaršanās punktu veidotā nogriežņa (hordas) garums ir

\frac{2 r \sqrt{l^{2} - r^{2}}}{l}

, bet šīs hordas attālums no centra -

\frac{r^{2}}{l}

. (No iepriekš apgūtā.)

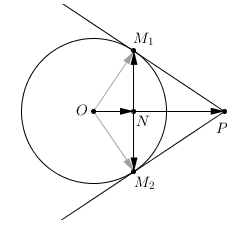
Tālāk būs parādīts, kā aprēķināt pieskaršanās punktu koordinātas, ja zināmas riņķa līnijas centra O koordinātas, riņķa līnijas rādiuss un koordinātas punktam P, no kura novilktas pieskares.

Ir zināmi vektoru ON un

O M_{1}

garumi:

ON = \frac{r^{2}}{l}

O M_{1} = O M_{2} = \frac{r \sqrt{l^{2} - r^{2}}}{l}

Vektoriem ON un OP sakrīt virzieni, atšķiras tikai garumi.

\frac{ON}{OP} = \frac{\frac{r^{2}}{l}}{l} = \frac{r^{2}}{l^{2}}

, tātad

\vec{ON} = \frac{r^{2}}{l^{2}} \vec{OP}

\vec{n}

apzīmēsim kādu vektoram

\vec{OP}

perpendikulāru vektoru ar tādu pašu garumu, un izteiksim ar tā palīdzību vektorus

\vec{N M_{1}}

\vec{N M_{2}}

. Viens no viņiem ir vērsts tāpat kā vektors

\vec{n}

(pieņemsim, ka

\vec{N M_{1}}

), otrs - pretēji. Turklāt

\frac{N M_{1}}{|\vec{n}|} = \frac{\frac{r \sqrt{l^{2} - r^{2}}}{l}}{l} = \frac{r \sqrt{l^{2} - r^{2}}}{l^{2}}

, tātad

\vec{N M_{1}} = \frac{r \sqrt{l^{2} - r^{2}}}{l^{2}} \vec{n}

\vec{N M_{2}} = - \frac{r \sqrt{l^{2} - r^{2}}}{l^{2}} \vec{n}

Attiecīgi

\vec{O M_{1}} = \vec{ON} + \vec{N M_{1}} = \frac{r^{2}}{l^{2}} \vec{OP} + \frac{r \sqrt{l^{2} - r^{2}}}{l^{2}} \vec{n}

\vec{O M_{2}} = \vec{ON} + \vec{N M_{2}} = \frac{r^{2}}{l^{2}} \vec{OP} - \frac{r \sqrt{l^{2} - r^{2}}}{l^{2}} \vec{n}

Vektora

\vec{n}

koordinātas var iegūt, apmainot vietām vektora

\vec{OP}

koordinātas un vienu no tām pareizinot ar -1. Garums paliks nemainīgs, bet abu vektoru skalārais reizinājums būs 0 - tātad tie būs perpendikulāri.

Zinot punktu O un P koordinātas, kā arī riņķa līnijas rādiusu, var aprēķināt attālumu l un vektoru

\vec{n}

\vec{OP}

koordinātas. Tad no tā var iegūt vektoru

O M_{1}

O M_{2}

koordinātas un, rezultātā, arī pieskaršanās punktu koordinātas.

Iepriekšējā teorija

Atgriezties tēmā

Nākamais uzdevums

Nosūtīt atsauksmi

Atradi kļūdu?

Sūti mums ziņu!

6. No punkta novilktas riņķa līnijas pieskares 2

Teorija