5. No punkta novilktas riņķa līnijas pieskares 1

Pieņemsim, ka riņķa līnijai no punkta (kas ir ārpus riņķa līnijas) ir novilkta pieskare, kas pieskaras riņķa līnijai punktā. Apzīmēsim riņķa līnijas centru ar O un rādiusu ar r, kā arī punktu, no kura vilkta pieskare, ar P un pieskaršanās punktu ar M. Un attālumu starp O un P ar l.

 

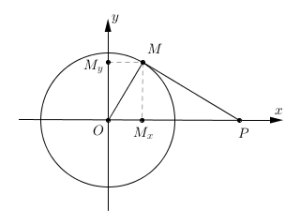
Rādiuss OM ir perpendikulārs pieskares nogrieznim MP, tātad trijstūris OMP ir taisnleņķa trijstūris un ${\mathit{OP}}^2={\mathit{OM}}^2+{\mathit{MP}}^2$ jeb $l^2=r^2+{\mathit{MP}}^2$. No tā var izteikt nogriežņa MP garumu - $\mathit{MP}=\sqrt{l^2-r^2}$.

 

Un tad var aprēķināt $M{M}_x$ garumu:

 

Pēc tam $M{M}_y$:

 

Hordas garums ir vienāds ar divkāršotu $M{M}_x$ garumu, bet tās attālums no centra - ar $M{M}_y$.

 

Ja riņķa līnijas centru novieto koordinātu sākumpunktā, bet punktu P uz Ox pozitīvā virziena, tad pieskaršanās punktu koordinātas ir $\left(\frac{r^2}{l};\frac{r\sqrt{l^2-r^2}}{l}\right)$ un $\left(\frac{r^2}{l};-\frac{r\sqrt{l^2-r^2}}{l}\right)$.