Hiperbola un tās vienādojums — teorija. Matemātika, Augstskola: 1. kurss.

Hiperbola un tās vienādojums

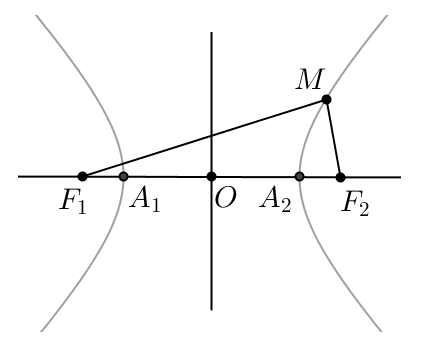
Hiperbolu veido punkti, kuriem attālumu starpība līdz diviem dotiem punktiem (hiperbolas fokusiem

F_{1}

F_{2}

) ir ar konstantu absolūto vērtību, kas ir mazāka par attālumu starp fokusiem.
(Zīmējumā -

|F_{1} M - F_{2} M| = Const

)

Svarīgi!

Ja hiperbolas fokusus novieto uz Ox ass un simetriski pret koordinātu sākumpunktu - punktos

F_{1} (- c; 0)

F_{2} (c; 0)

, un konstanto attālumu starpības moduli apzīmē ar 2a, tad hiperbolas vienādojums ir

\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1

(kur

b^{2} = c^{2} - a^{2}

).
Šo vienādojumu sauc par hiperbolas kanonisko vienādojumu.

Šo vienādojumu iegūst šādi.

Punkta

M (x; y)

attālums līdz punktam

F_{1} (- c; 0)

\sqrt{{(x + c)}^{2} + y^{2}}

, attālums līdz punktam

F_{2} (c; 0)

\sqrt{{(x - c)}^{2} + y^{2}}

. No tā iegūst vienādojumu

|\sqrt{{(x + c)}^{2} + y^{2}} - \sqrt{{(x - c)}^{2} + y^{2}}| = 2 a

, kuru pārveido:

\begin{array}{l} \sqrt{{(x + c)}^{2} + y^{2}} = \sqrt{{(x - c)}^{2} + y^{2}} \pm 2 a \\ {(x + c)}^{2} + y^{2} = {(x - c)}^{2} + y^{2} + 4 a^{2} \pm 4 a \sqrt{{(x - c)}^{2} + y^{2}} \\ cx - a^{2} = \pm a \sqrt{{(x - c)}^{2} + y^{2}} \\ c^{2} x^{2} - 2 a^{2} cx + a^{4} = a^{2} x^{2} - 2 a^{2} cx + a^{2} c^{2} + a^{2} y^{2} \\ (c^{2} - a^{2}) x^{2} - a^{2} y^{2} = a^{2} (c^{2} - a^{2}) \\ b^{2} x^{2} - a^{2} y^{2} = a^{2} b^{2} \\ \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 \end{array}

Atradi kļūdu?

1. Hiperbola un tās vienādojums